Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O’) có đường kính CB. Hai đường tròn (O) và (O’) có vị trí tương đối như thế nào đối với nhau?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 10 2018
a) Ta có: OO' = OB – O'B
⇒ Hai đường tròn (O) và (O') tiếp xúc trong tại B
CM
20 tháng 2 2018
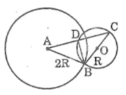
Ta có: R < OA < 3R ⇔ 2R – R < OA < 2R + R
Suy ra hai đường tròn (O ; R) và (A ; 2R) cắt nhau
8 tháng 12 2023
a: OI+IB=OB
=>OI=OB-IB
=>\(OI=R-r\)
=>Hai đường tròn (O) và (I) tiếp xúc trong với nhau tại B
b: Ta có: ΔODE cân tại O
mà OH là đường cao
nên H là trung điểm của DE
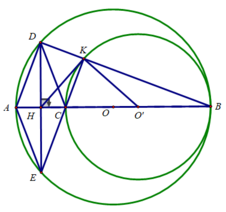
Xét tứ giác ADCE có
H là trung điểm chung của AC và DE
=>ADCE là hình bình hành
Hình bình hành ADCE có AC\(\perp\)DE
nên ADCE là hình thoi
c: Xét (I) có
ΔCKB nội tiếp
CB là đường kính
Do đó: ΔCKB vuông tại K
=>CK\(\perp\)KB tại K
=>CK\(\perp\)DB tại K
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE\(\perp\)BE tại E
Ta có: ADCE là hình thoi
=>AE//CD
mà AE\(\perp\)EB
nên CD\(\perp\)EB
Xét ΔDEB có
BH,DC là các đường cao
BH cắt DC tại C
Do đó: C là trực tâm của ΔDEB
=>EC\(\perp\)DB
mà CK\(\perp\)DB
và EC,CK có điểm chung là C
nên E,C,K thẳng hàng
d:
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
Xét tứ giác DHCK có \(\widehat{DHC}+\widehat{DKC}=90^0+90^0=180^0\)
nên DHCK là tứ giác nội tiếp
=>\(\widehat{HKC}=\widehat{HDC}\)
mà \(\widehat{HDC}=\widehat{ADH}\)(DH là phân giác của góc ADC do ADCE là hình thoi)
nên \(\widehat{HKC}=\widehat{ADH}\)
mà \(\widehat{ADH}=\widehat{ABD}\left(=90^0-\widehat{DAB}\right)\)
nên \(\widehat{HKC}=\widehat{ABD}\)
Ta có: IC=IK
=>ΔICK cân tại I
=>\(\widehat{ICK}=\widehat{IKC}\)
\(\widehat{HKI}=\widehat{HKC}+\widehat{IKC}\)
\(=\widehat{ABD}+\widehat{ICK}\)
\(=\widehat{KBC}+\widehat{KCB}=90^0\)
=>HK\(\perp\)KI tại K
=>HK là tiếp tuyến tại K của (I)
CM
15 tháng 9 2017
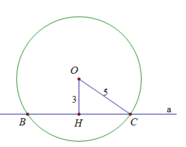
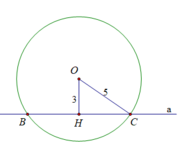
Đường thẳng a cắt đường tròn (O) tại 2 điểm phân biệt, vì khoảng cách d < R
CM
3 tháng 9 2019
a) Đường thẳng a cắt đường tròn (O) tại 2 điểm phân biệt, vì khoảng cách d < R
b) Xét tam giác OHC vuông tại H có:
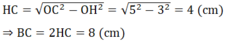
Vì O, O’ và B thẳng hàng nên: O’B < OB => O’ nằm giữa O và B
Ta có: OO’ = OB - O’B
Vậy đường tròn (O’) tiếp xúc với đường tròn (O) tại B