Cho hình thang ABCD có AB // CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
Chứng minh rằng: M D D A = N C B C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 11 2018
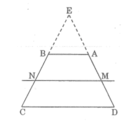
Gọi E la giao điểm của AD va BC
Trong tam giác EMN, ta có: AB // MN (gt)
Suy ra: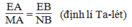 
Hay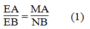 
Trong tam giác EDC, ta có: AB // CD (gt)
Suy ra: 
Hay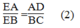 
Từ (1) và (2) suy ra :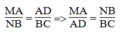 
27 tháng 1 2023
a: Gọi K là giao của AD và BC
Xét ΔKDC có AB//DC
nên KA/AD=KB/BC
=>KA/KB=AD/BC
Xét ΔKMN có AB//MN
nên KA/AM=KB/BN
=>KA/KB=AM/BN
=>AM/BN=AD/BC
=>AM/AD=BN/BC
b: AM/AD=BN/BC
=>AD/AM=BC/BN
=>AD/AM-1=BC/BN-1
=>\(\dfrac{AD-AM}{AM}=\dfrac{BC-BN}{BN}\)
=>DM/AM=NC/BN
=>MA/MD=BN/NC
c: AM/AD=BN/BC
=>AM/AD-1=BN/BC-1
=>(AM-AD)/AD=(BN-BC)/BC
=>-MD/AD=-CN/BC
=>MD/AD=CN/BC
CM
5 tháng 12 2017
Trong ΔDAB, ta có: OM // AB (gt)
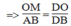(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
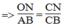(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: 
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: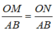 
Vậy: OM = ON
21 tháng 1 2021
Xét Tam giác ADB: MN // AB (gt)
Suy ra: DN/DB = MN/AB (Hệ quả định lí Talét) (1)
Xét Tam giác ACB: PQ // AB (gt)
Suy ra: CQ/CB = PQ/AB (Hệ quá định lí Talét) (2)
Ta có: NQ sog sog AB (gt)
AB sog sog CD (gt)
Suy ra: NQ sog sog CD (cùng sog sog AB)
Xét Tam giác BDC: NQ sog sog CD (cmt)
Suy ra: DN/DB = CQ/CB (Định lí Talét) (3)
Từ (1), (2) và (3) suy ra: MN/AB = PQ/AB
Suy ra: MN = PQ (đpcm).
AH
Akai Haruma
Giáo viên
25 tháng 2 2021
"Hai đường chéo cắt nhau tại O và song song với đáy AB....". Câu này không đúng lắm. Bạn xem lại đề.
CM
12 tháng 8 2017
Trong ΔADB, ta có: MN // AB (gt)
Suy ra: 
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: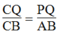 
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: 
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra 
hay MN = PQ.
CM
16 tháng 6 2019
Trong ΔADB, ta có: MN // AB (gt)
Suy ra: 
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: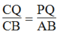 
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: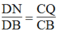 
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra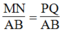 
hay MN = PQ.
Ta có: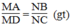
Áp dụng tính chất dãy tỉ số bằng nhau ta có: