Vật AB có độ cao h được đặt vuông góc trước một thấu kính hội tụ tiêu cự f như hình 42-43.5 SBT. Điểm A nằm trên trục chính cách thấu kính một khoảng d = 2f. Vận dụng kiến thức hình học, tính chiều cao h' của ảnh theo h và tính khoảng cách từ d' từ ảnh đến thấu kính theo...
Đọc tiếp
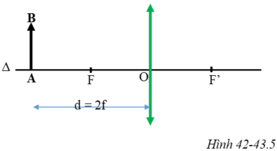
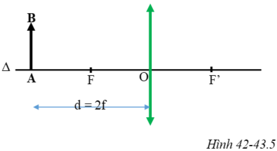
Vật AB có độ cao h được đặt vuông góc trước một thấu kính hội tụ tiêu cự f như hình 42-43.5 SBT. Điểm A nằm trên trục chính cách thấu kính một khoảng d = 2f. Vận dụng kiến thức hình học, tính chiều cao h' của ảnh theo h và tính khoảng cách từ d' từ ảnh đến thấu kính theo d.
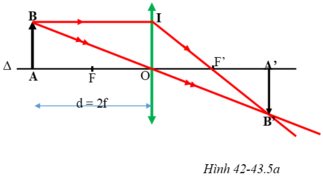
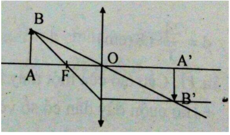
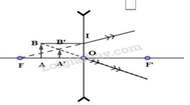
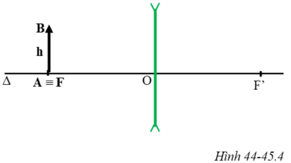
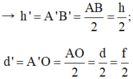
Trên hình 42-43.5a, xét hai cặp tam giác đồng dạng:
ΔABO và ΔA’B’O; ΔA’B’F’ và ΔOIF’.
Từ hệ thức đồng dạng được: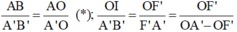
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
Chia cả hai vế của (1) cho tích d.d’.f ta được:
(đây được gọi là công thức thấu kính cho trường hợp ảnh thật)
Thay d = 2f, ta tính được: OA’ = d’ = 2f = d
Thay vào (*) ta được: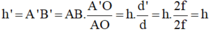
Vậy d’ = d; h’ = h.