Trong không gian với hệ tọa độ Oxyz cho tam giác ABC với A(1;0;0), B(3;2;4), C(0;5;4). Tìm tọa độ điểm M thuộc mặt phẳng Oxy sao cho nhỏ nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
26 tháng 7 2019
Đáp án A
Gọi D là chân đường phân giác góc B của tam giác ABC . Theo tính chất đường phân giác ta có : 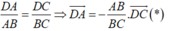
![]()
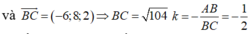
Từ (*) ta có, điểm D chia đoạn thẳng AC theo tỷ số k nên D có toạ độ
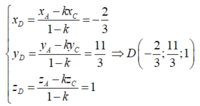
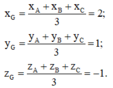
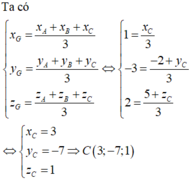
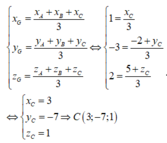
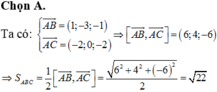
Đáp án là B