Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y = x 4 + 2 m x 2 + 1 có ba điểm cực trị tạo thành tam giác vuống cân
A. m = − 3 3
B. m = -1
C. m = − 1 ; m = 3 3
D. m = − 3 3 ; m = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Xét hàm số y = x 4 − 2 m x 2 + 2 m + m 4 , có y ' = 4 x 3 − 4 m x , ∀ x ∈ ℝ
Phương trình y ' = 0 ⇔ 4 x 3 − 4 m x = 0 ⇔ x x 2 − m = 0 ⇔ x = 0 x 2 = m *
Để hàm số có ba điểm cực trị ⇔ * có 2 nghiệm phân biệt khác 0
Khi đó, gọi A 0 ; 2 m + m 4 , B m ; m 4 − m 2 + 2 m , C − m ; m 4 − m 2 + 2 m là tọa độ ba điểm cực trị của đồ thị hàm số.
Tam giác ABC đều ⇔ A B 2 = B C 2 ⇔ m + m 4 = 4 m ⇔ m 4 = 3 m ⇔ m = 3 3

Đáp án C

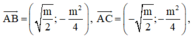
Tam giác ABC cân tại A, do đó để tam giác ABC vuông cân
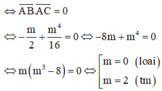

Chọn D
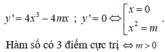
Khi đó đồ thị hàm số có 3 điểm cực trị là:
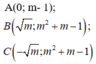
Vì B, C đối xứng với nhau qua trục tung nên B C ⊥ O A
Do đó O là trực tâm tam giác:
![]()
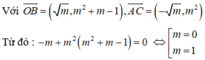
Kết hợp điều kiện, vậy m = 1 là giá trị cần tìm
Đáp án là B