Có bao nhiêu giá trị thực của tham số m để GTLN của hàm số trên đoạn bằng 4?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

Chọn D
Phương pháp:
Sử dụng: Hàm số y = ax+b đồng biến ⇔ a > 0, từ đó kết hợp điều kiện đề bài để tìm các giá trị của m.
Cách giải:
Hàm số y = (m-2)x + 2 đồng biến trên ℝ ⇔ m - 2 > 0 ⇔ m > 2
Mà ![]()
![]() => có 2016 giá trị nguyên của m thỏa mãn đề bài.
=> có 2016 giá trị nguyên của m thỏa mãn đề bài.
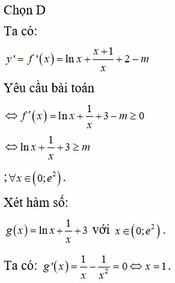

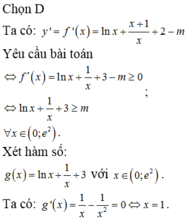


Đáp án B.
Phương pháp:
Sử dụng cách vẽ đồ thị hàm số y = f x
Cách giải:
Xét hàm số y = x 2 + 2 x + m − 4 = f x có:
y ' = 2 x + 2
y ' = 0 ⇔ x = − 1
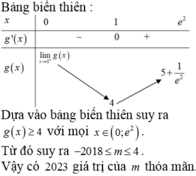
Bảng biến thiên:
+) m ≥ 5 :
M a x − 2 ; 1 x 2 + 2 x + m − 4 = f 1 = m − 1 = 4 ⇒ m = 5
(Thỏa mãn)
+) 4 ≤ m < 5 :
M a x − 2 ; 1 x 2 + 2 x + m − 4 = M a x m − 1 ; 5 − m = 4
Mà
m − 1 > 5 − m , ∀ m ∈ 4 ; 5 ⇒ m − 1 = 4 ⇒ m = 5
(loại)
+) 1 ≤ m < 4 :
M a x − 2 ; 1 x 2 + 2 x + m − 4 = M a x 5 − m ; m − 1 = 4.
m ∈ − 1 ; 3 ⇒ max y = 5 − m = 4 ⇔ m = 1 t m
m ∈ − 1 ; 3 ⇒ max y = m − 1 = 4 ⇔ m = 5 k t m
+) m < 1 :
M a x − 2 ; 1 x 2 + 2 x + m − 4 = 5 − m = 4 ⇒ m = 1
(Không thỏa mãn)
Vậy m ∈ 4 ; 1 , có hai giá trị của m thỏa mãn.