Cho ABC tam giác nhọn ( AB song song AC ) Đường tròn tâm O có đường kính BC cắt AB ;
AC lần lượt tại E ; F .
a) C/m: tam giác BECvà tam giácBFC là các tam giác vuông
b) Gọi K là giao điểm của BF và CE. Chứng minh: AKBC
c) Chứng minh: 4 điểm A; E; K; F cùng thuộc một đường tròn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 3 2016
a) Xét tam giác BEC
Ta có :
tam giác BEC nt (O)
BC đường kính
=> tam giác BEC vuông tại E
Xét tam giác BDC
Ta có :
tam giác BDC nt (o)
BC đường kính
=> tam giác BDC vuông tại D
Ta có:
góc BEC vuông tại E
góc BDC vuông tại D
Mà EC cắt DB tại H
=> H là trực tâm
=> AH vuông góc Với BC tại F
c) Xét tg BEHF
Ta có
góc BEH= 90 độ
góc BFH = 90 độ
=> góc BEC + góc BDC = 90 độ + 90 độ = 180 độ
=> tg BEHF nt(tổng 2 góc đối bằng 180 độ )
Ta có: B, E, D, F thuộc (O)
=> tg BEDF nt (O)
=> góc EBD = góc EFD ( 1 )
ta có: tg BEHF nt
=> góc EBH = góc EFH ( 2 )
từ (1) và (2)
=> góc EFD = góc EFH
=> AF // AF
2 tháng 6 2017
tứ giác ABHE nooj tiếp => góc ABH = góc HED (1)
Mà góc ADC= gcos ABC (2)
tỪ 1 VÀ 2 => HED = EDC => EH// DC
2 tháng 6 2017
TỨ GIÁC ABDC nt =>GÓC BAD +GÓC HED =180 ĐỘ
MẶT KHÁC GÓC BAD =BCD =1/2 CUNG BD
TỪ ĐÓ=>>HE // DC
14 tháng 4 2023
a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc DFC=góc EBC
góc EFC=góc DAC
góc EBC=góc DAC
=>góc DFC=góc EFC
23 tháng 11 2023
a: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)
=>ADHE là tứ giác nội tiếp đường tròn đường kính AH
=>A,D,H,E cùng nằm trên đường tròn đường kính AH
b: Xét (O) có
ΔACK nội tiếp
AK là đường kính
Do đó: ΔACK vuông tại C
=>KC\(\perp\)AC
mà HD\(\perp\)AC
nên KC//HD
20 tháng 5 2018
Ai trả lời hộ điiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiinhanh lênnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
6 tháng 6 2018
a) Ta có: DE là tiếp tuyến của (O) nên ^ODE=900 . Mà OH vuông góc BE
=> ^OHE=900 => ^ODE=^OHE.
Xét tứ giác OHDE: ^OHE=^ODE=900 => Tứ giác OHDE nội tiếp đường tròn. (đpcm).
b) Dễ thấy ^EDC=^EBD (T/c góc tạo bởi tiếp tuyến và dây cung)
=> \(\Delta\)ECD ~ \(\Delta\)EDB (g.g) => \(\frac{ED}{EB}=\frac{EC}{ED}\Rightarrow ED^2=EC.EB.\)(đpcm).
c) Tứ giác OHDE nội tiếp đường tròn (cmt) => ^OEH=^ODH.
Lại có: CI//OE => ^OEH=^ICH => ^ICH=^ODH hay ^ICH=^IDH
=> Tứ giác HICD nội tiếp đường tròn => ^HID=^HCD=^BCD
Do tứ giác ABDC nội tiếp (O) => ^BCD=^BAD.
Do đó ^HID=^BAD. Mà 2 góc bên ở vị trí đồng vị => HI//AB (đpcm).
d) Gọi giao điểm của tia CI với AB là P.
Ta thấy: Đường tròn (O) có dây cung BC và OH vuông góc BC tại H => H là trung điểm BC.
Xét \(\Delta\)BPC: H là trung điểm BC; HI//BP (HI//AB); I thuộc CP => I là trung điểm CP => IC=IP (1)
Theo hệ quả của ĐL Thales; ta có: \(\frac{IP}{DM}=\frac{AI}{AD};\frac{IC}{DN}=\frac{AD}{AI}\Rightarrow\frac{IP}{DM}=\frac{IC}{DN}\)(2)
Từ (1) và (2) => DM=DN (đpcm).
HC
2 tháng 9 2020
Bài 1 : Bài giải
Hình tự vẽ //
a) Ta có DOC = cung DC
Vì DOC là góc ở tâm và DAC là góc chắn cung DC
=>DOC = 2 . AOC (1)
mà tam giác AOC cân =>AOC=180-2/AOC (2)
Từ (1) ; (2) ta được DOC + AOC = 180
b) Góc ACD là góc nội tiếp chắn nữa đường tròn
=>ACD=90 độ
c) c) HC=1/2*BC=12
=>AH=căn(20^2-12^2)=16
Ta có Sin(BAO)=12/20=>BAO=36.86989765
=>AOB=180-36.86989765*2=106.2602047
Ta có AB^2=AO^2+OB^2-2*OB*OA*cos(106.2602047)
<=>AO^2+OA^2-2OA^2*cos(106.2602047)=20^2
=>OA=12.5
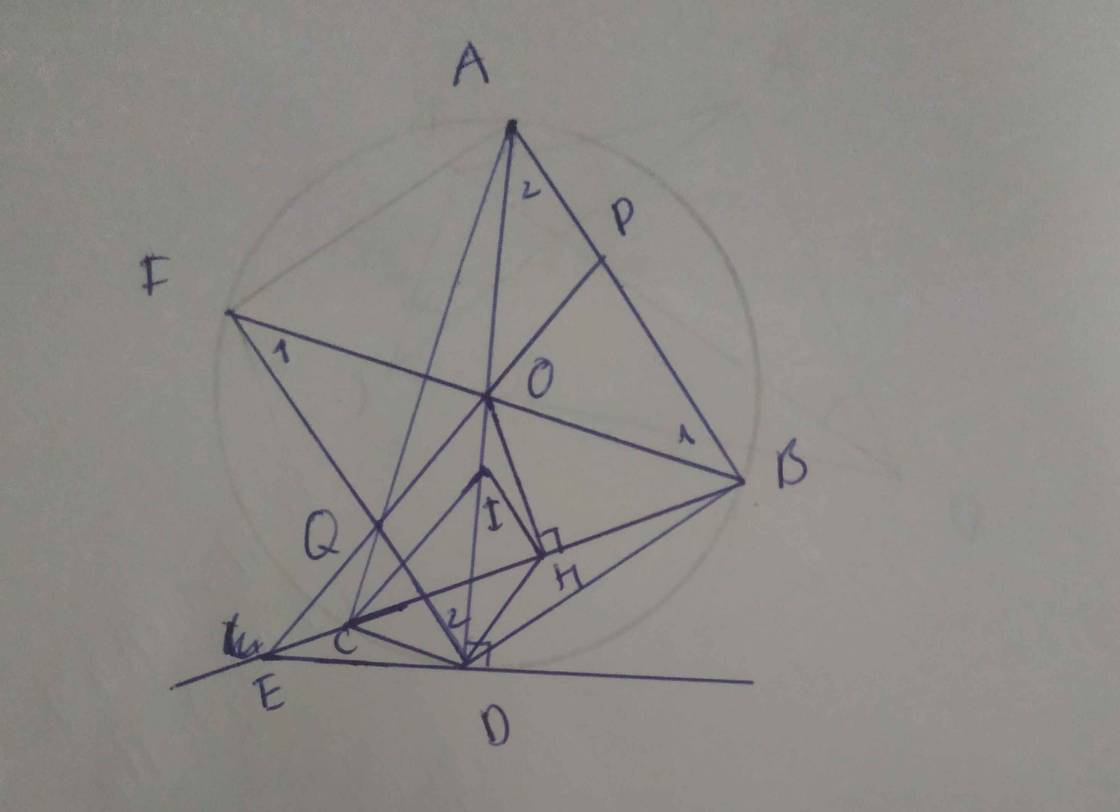
mình cần gấp ạ mình xin cảm ơn ạ