Cho hàm y = f(x) thỏa mãn xy ' = y ylnx − 1 . Khi đó f(x) bằng
A. 1 1 + x
B. 1 1 + x + ln x
C. ln x + 1
D. x + 1 ln x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét x=0,y=1 ta có f(1)=f(0)f(1)-f(1)+2 (a)
xét x=1,y=0 ta có f(1)=f(1)f(0)-f(0)+1 (b)
xét x=0,y=0 ta có f(1)=f(0)f(0)-f(0)+2 (c)
Lấy (a)-(b) suy ra f(1)=f(0)+1 thay vào (c) ta được f(0)+1=f(0)f(0)-f(0)+2 <=>f(0).f(0)-2f(0)+1=0 <=> f(0)=1 =>f(1)=f(0)+1=2
xét x=1 ta có f(y+1)=f(1)f(y)-f(y)-1+2=f(y)+1
f(y+1)=f(y)+1=f(y-1)+1+1=...F(y-n)+1+n (n là số tự nhiên)
vậy f(2018)=f(2017+1)=f(2017-2016)+1+2016( lấy n=2016)=f(1)+2017=2019
vậy biểu thức có giá trị là 10.2019+1=20191
Đáp án A
Phương pháp giải:
Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn
Lời giải:
Ta có 
suy ra f(x) là hàm số nghịch biến trên [a;b]
Mà 
. Vậy 
Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn
Ta có f’ (x) = -x2-1< 0 với a< x< b ; suy ra hàm số y= f( x) là hàm số nghịch biến trên [ a; b].
Mà a< b nên f(a) > f( b)
Vậy m i n [ a ; b ] f ( x ) = f ( b )
Chọn C.
\(\Leftrightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}+2x=lnx\Rightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}=lnx-2x\)
Lấy nguyên hàm 2 vế:
\(\Rightarrow\int\dfrac{f'\left(x\right)}{f\left(x\right)}dx=\int\left(lnx-2x\right)dx\)
\(\Rightarrow ln\left|f\left(x\right)\right|=x\left(lnx-1\right)-x^2+C\)
Thay \(x=1\)
\(\Rightarrow ln\left|f\left(1\right)\right|=-2+C\Rightarrow C=2\)
\(\Rightarrow ln\left|f\left(x\right)\right|=x\left(lnx-1\right)-x^2+2\)
\(\Rightarrow\left|f\left(x\right)\right|=e^{x\left(lnx-1\right)-x^2+2}\)
\(\Rightarrow\left|f\left(2\right)\right|\)
.
.
.
.
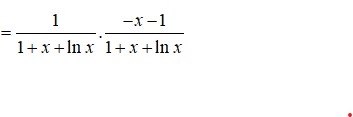
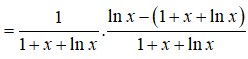
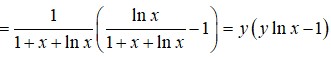
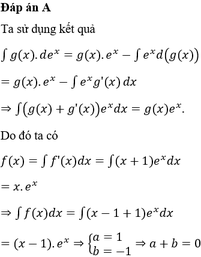
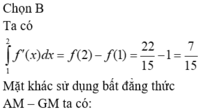
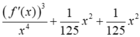
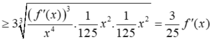
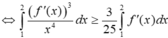
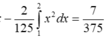
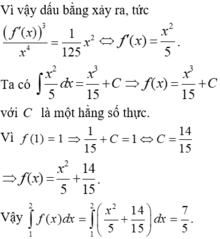
Đáp án B
Thay y = 1 1 + x + ln x thỏa mã