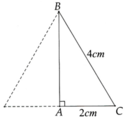
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V 1 . Tam giác ABC quay xung
quanh trục d được khối tròn xoay có thể tích là V 2 . Tính tỉ số V 1 V 2 .
A. 2 3
B. 1 3
C. 3
D. 3 2

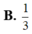
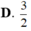

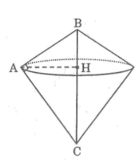




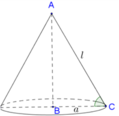
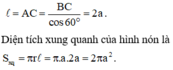


Chọn C.
Phương pháp:
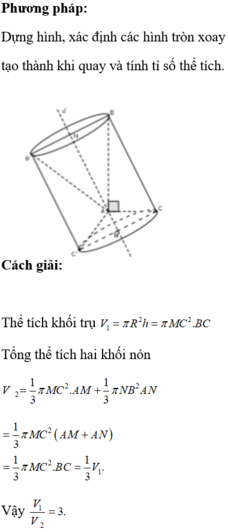
Dựng hình, xác định các hình tròn xoay tạo thành khi quay và tính tỉ số thể tích.
Cách giải: