Gọi x,y là các số thực dương thỏa mãn điều kiện l o g 9 x = l o g 6 y = l o g 4 ( x + y ) và x y = - a + b 2 , với a,b là hai số nguyên dương. Tính a.b
A. a.b=5
B. a.b=1
C. a.b=8
D. a.b=4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
2 tháng 6 2019
Đúng(0)
Những câu hỏi liên quan
2 tháng 1 2021
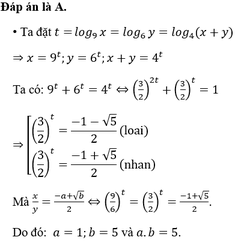
3: \(P=\dfrac{x}{\left(x+y\right)+\left(x+z\right)}+\dfrac{y}{\left(y+z\right)+\left(y+x\right)}+\dfrac{z}{\left(z+x\right)+\left(z+y\right)}\le\dfrac{1}{4}\left(\dfrac{x}{x+y}+\dfrac{x}{x+z}\right)+\dfrac{1}{4}\left(\dfrac{y}{y+z}+\dfrac{y}{y+x}\right)+\dfrac{1}{4}\left(\dfrac{z}{z+x}+\dfrac{z}{z+y}\right)=\dfrac{3}{2}\).
Đẳng thức xảy ra khi x = y = x = \(\dfrac{1}{3}\).
CM
10 tháng 1 2018
Đáp án A
Ta có log 9 x = log 6 x = log 4 x + y = t ⇔ x = 9 t y = 6 t ; x + y = 4 t
Khi đó 9 t + 6 t = 4 t ⇔ 3 2 t 2 + 3 2 t - 1 = 0 ⇔ x y = 3 2 t = - 1 + 5 2 ⇒ a = 1 b = 5 .
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 2 2022
Hướng dẫn: đặt \(A=\dfrac{y^4}{\left(x^2+y^2\right)\left(x+y\right)}+\dfrac{z^4}{\left(y^2+z^2\right)\left(y+z\right)}+\dfrac{x^4}{\left(z^2+x^2\right)\left(z+x\right)}\)
Khi đó \(F-A=x-y+y-z+z-x=0\Rightarrow F=A\)
\(\Rightarrow2F=F+A=\sum\dfrac{x^4+y^4}{\left(x^2+y^2\right)\left(x+y\right)}\ge\sum\dfrac{\left(x^2+y^2\right)^2}{2\left(x^2+y^2\right)\left(x+y\right)}\ge\sum\dfrac{\left(x+y\right)^2\left(x^2+y^2\right)}{4\left(x^2+y^2\right)\left(x+y\right)}\)
\(\Rightarrow2F\ge\dfrac{x+y+z}{2}\Rightarrow F\ge\dfrac{x+y+z}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2021
\(4\le\left(\sqrt{x}+1\right)\left(\sqrt{y}+1\right)\le\dfrac{1}{4}\left(\sqrt{x}+\sqrt{y}+2\right)^2\)
\(\Rightarrow\sqrt{x}+\sqrt{y}+2\ge4\)
\(\Rightarrow2\le\sqrt{x}+\sqrt{y}\le\sqrt{2\left(x+y\right)}\Rightarrow x+y\ge2\)
\(\Rightarrow P\ge\dfrac{\left(x+y\right)^2}{x+y}=x+y\ge2\)
Dấu "=" xảy ra khi \(x=y=1\)
7 tháng 5 2021
Dạ có thể diễn đạt theo cách dễ hiểu cho đứa ngu lâu dốt bền như em được không ạ ? ._.
GB
23 tháng 5 2022
a) Ta có: \(\widehat{xOy}=140^0\)
\(\widehat{xOA}=\widehat{yOB}=90^0\) ( do \(OA\perp Ox,OB\perp Oy\) )
\(\Rightarrow\widehat{AOB}=360-\left(\widehat{xOy}+\widehat{xOA}+\widehat{yOB}\right)\)
\(\Leftrightarrow\widehat{AOB}=360^0-\left(140^0+90^0+90^0\right)\)
\(\Leftrightarrow\widehat{AOB}=40^0\)
\(OM\) là tia phân giác của \(\widehat{xOy}\)
\(\Rightarrow\widehat{xOM}=\widehat{MOy}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}.140^0=70^0\)
\(OM'\) là tia đối của \(OM\Rightarrow\widehat{MOM'}=180^0\)
Mà \(OA\) nằm ngoài \(\widehat{xOy}\) và \(OA\perp Ox\) nên \(\widehat{MOM'}=\widehat{MOx}+\widehat{xOA}+\widehat{AOM'}\)
Do đó \(\widehat{AOM'}=\widehat{MOM'}-\left(\widehat{MOx}+\widehat{xOA}\right)\) \(\Rightarrow\widehat{AOM'}=180^0-\left(70^0+90^0\right)=20^0\) \(\left(1\right)\)
Mặt khác \(Oy\) nằm giữa \(OB\) và \(OM\) nên \(\widehat{MOB}=\widehat{MOy}+\widehat{yOB}=70^0+90^0=160^0\)
\(\Rightarrow\widehat{MOB}< \widehat{MOM'}\)
Do đó \(OB\) và \(Oy\) nằm cùng nửa mặt phẳng bờ \(MM'\)
\(Ox\) nằm giữa \(OA\) và \(OM\) nên\(\widehat{MOA}=\widehat{MOx}+\widehat{xOA}=70^0+90^0=160^0\)
\(\Rightarrow\widehat{MOA}< \widehat{MOM'}\)
Do đó tia \(OA\) và \(Ox\) nằm cùng nửa mặt phẳng bờ \(MM'\)
Nên \(OM'\) nằm giữa \(OA\) và \(OB\)
\(\Rightarrow\widehat{AOB}=\widehat{AOM'}+\widehat{M'OB}\Rightarrow\widehat{M'OB}=\widehat{AOB}-\widehat{AOM'}=40^0-20^0=20^0\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta có: \(\widehat{M'OB}=\widehat{AOM'}=20^0=\dfrac{1}{2}\widehat{AOB}\)
Suy ra \(OM'\) là tia phân giác của góc \(\widehat{AOB}\)
b) Ta có: \(\widehat{MOx}< \widehat{MOA}< \widehat{MOM'}\) nên \(OA\) nằm giữa \(Ox\) và \(OM'\)
Mà \(OM'\) là tia phân giác của góc \(\widehat{AOB}\)
Suy ra \(OA\) nằm giữa \(Ox\) và \(OB\)
Vậy \(\widehat{xOB}=\widehat{xOA}+\widehat{AOB}=90^0+40^0=130^0\)