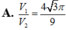
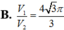
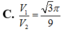
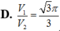
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
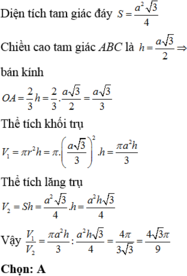
Phương pháp:
- Thể tích khối trụ 
với r là bán kính đáy.
- Tính thể tích khối lăng trụ V 2 = Sh với S là diện tích đáy.
Cách giải:
Diện tích tam giác đáy 
Chiều cao tam giác ABC là h = a 3 2
=> bán kính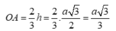 
Thể tích khối trụ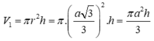 
Thể tích lăng trụ 
Vậy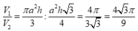 
Chọn: A
Đáp án A
Diện tích của tam giác đều cạnh a là a 2 3 4 . Lăng trụ tm giác đều các cạnh bên vuông góc với đáy nên thể tích của lăng trụ đã cho V = a . a 2 3 4 = a 3 3 4
Đáp án B
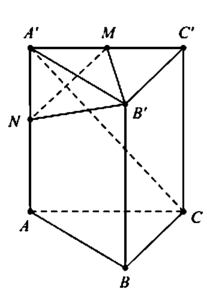Gọi M là trung điểm A’C’. Ta có
B
'
M
⊥
A
C
C
'
A
'
⇒
B
'
M
⊥
A
'
C
.
Suy ra M ∈ m p P . Kẻ M N ⊥ A ' C ( N ∈ A A ' ) ⇒ N ∈ m p P
Thiết diện cắt bởi mặt phẳng (P) và lăng trụ là tan giác B’MN
Hai tam giac A’C’C và NA’M đồng dạng ⇒ A ' N = 1 2 A ' M = a 4
Thể tích tứ diện A'B'MN là V 1 = 1 3 A ' N . S ∆ A ' B ' M = a 3 3 96
Thể tích lăng trụ là V = A A ' . S ∆ A B C = a 3 3 2 . Vậy V 1 V 2 = 1 47 .
