Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Gọi số tiền ban đầu là T. Sau n năm, số tiền thu được là:
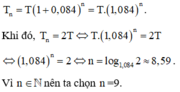
Đáp án A
Gọi số tiền ban đầu là a thì ta có 
Suy ra sau 9 năm thì người đó sẽ có số tiền gấp đôi số tiền ban đầu
Đáp án A
Ta có T = A 1 + 8 , 4 % n mà T = 2 A suy ra 1 , 084 n = 2 ⇒ n = log 1 , 084 2 ≈ 8 , 6 năm
Giả sử: số tiền ban đầu đem gửi là a (đồng)
Từ yêu cầu bài ra thì số tiền thu được là 2a (đồng)
Vì một năm lãi suất là 8,4%, mà một năm có 12 tháng nên số lãi một tháng là:
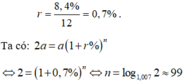
Chọn D
Giả sử: số tiền ban đầu đem gửi là a (đồng)
Từ yêu cầu bài ra thì số tiền thu được là 2a (đồng)
Vì một năm lãi suất là 8,4%, mà một năm có 12 tháng nên số lãi một tháng là:
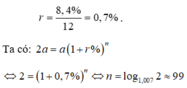
Chọn D
Đáp án C
Theo công thức lãi kép ta có T = A 1 + r n với T là số tiền cả gốc cả lãi thu được, A là số tiền ban đầu, r là số tiền lãi suất, n là kì hạn
Để sổ tiền tăng gấp đôi thì T = 2 A ⇒ 2 A = A 1 + r n ⇔ 2 = 1 + 0 , 075 n ⇔ n = log 1075 2 ≈ 9 , 6 năm
Vậy cẩn 10 năm để sổ tiền tâng gấp đôi
Chọn C
Gọi A là số tiền gửi ban đầu, n là số năm gửi.
Theo bài ra: Sau 1 năm, số tiền cả vốn lẫn lãi là : A + A. 8,4% =A. 1,084.
Sau 2 năm, số tiền cả vốn lẫn lãi là: A.1,084 + A. 1,084.8,4% = A. 1,084^2.
Sau n năm, số tiền cả vốn lẫn lãi là A. 1,084^n.
Số tiền này bằng 2 lần ban đầu nên: A. 1,084^n = 3A
ð n = ~ 14
Đáp án là B