Một nhóm học sinh gồm 5 bạn nam, và 3 bạn nữ cùng đi xem phim, có bao nhiêu cách xếp 8 bạn vào 8 ghế hàng ngang sao cho 3 bạn nữ ngồi cạnh nhau?
A.5!.3!
B. 8! – 5.3!.
C.6!.3!.
D. 8 ! 3 ! .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 12 2019
Chọn D
Số phần tử của không gian mẫu: 
Gọi A là biến cố: “cặp sinh đôi ngồi cạnh nhau và nam nữ không ngồi đối diện nhau”.
Ta tính n() như sau:
Đánh số các ghế ngồi của 8 học sinh như hình vẽ sau:
- Để xếp cho cặp sinh đôi ngồi cạnh nhau có 6 cách.
- Mỗi cách như vậy có cách đổi chỗ.
- Với mỗi cách xếp cặp sinh đôi, ví dụ: Cặp sinh đôi ở vị trí 1 và 2.
Do nam nữ không ngồi đối diện nên:
+ Vị trí 5 và 6 đều có 3 cách.
+ Vị trí 3 có 4 cách, vị trí 7 có 1 cách.
+ Vị trí 4 có 2 cách, vị trí 8 có 1 cách.
Suy ra n(A) = 6.2.3.3.4.1.2.1 = 864
5 tháng 1 2023
a: Số cách xếp là: \(A^5_{10}=30240\left(cách\right)\)
b: TH1: 3 nam 2 nữ
=>Số cách xếp là: \(3!\cdot2!\cdot2!\)(cách)
TH2: 2 nam 3 nữ
=>Số cách xếp là: 2!*3!*2!(cách)
TH3: 1 nam 4 nữ
=>Số cách xếp là 1!*4!*2!(cách)
TH4: 0 nam 5 nữ
=>Số cách xếp là 5!(cách)
=>Số cách là \(2!\cdot2!\cdot3!+2!\cdot2!\cdot3!+1!\cdot4!\cdot2!+5!\left(cách\right)\)
c: Số cách chọn 2 nữ trong 7 nữ là:
\(C^2_7\left(cách\right)\)
Số cách xếp 3 nam và 2 nữ là:
\(3!\cdot3!\left(cách\right)\)
=>Số cách là: \(C^2_7\cdot3!\cdot3!\left(cách\right)\)
CM
13 tháng 8 2018
Để xác định, các ghế được đánh số từ 1 đến 10 tính từ trái sang phải.
a) Nếu các bạn nam ngồi ở các ghế ghi số lẻ thì các bạn nữ ngồi ở các ghế còn lại. Có 5! cách xếp bạn nam, 5! cách xếp bạn nữ. Tất cả có 5 ! 2 cách xếp.
Nếu các bạn nam ngồi ở các ghế ghi số chẵn, các bạn nữ ngồi ở các ghế còn lại thì có 5 ! 2 cách xếp nam và nữ.
Vậy có tất cả 2. 5 ! 2 cách xếp nam nữ ngồi xen kẽ nhau.
b) Các bạn nam được bố trí ngồi ở các ghế từ k đến k + 4, k = 1, 2, 3, 4, 5, 6. Trong mỗi trường hợp có 5 ! 2 cách xếp nam và nữ.
Vậy có 6. 5 ! 2 cách xếp mà các bạn nam ngồi cạnh nhau.
CM
15 tháng 7 2019
a) Xếp 6 nam vào 6 ghế cạnh nhau. Có 6! cách.
Giữa các bạn nam có 5 khoảng trống cùng hai đầu dãy, nên có 7 chỗ có thể đặt ghế cho nữ.
Bây giờ chọn 4 trong 7 vị trí để đặt ghế. Có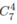 
cách.
Xếp nữ vào 4 ghế đó. Có 4! cách.
Vậy có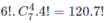 
cách xếp mà không có hai bạn nữ nào ngồi cạnh nhau.
b) Xếp 6 ghế quanh bàn tròn rồi xếp nam vào ngồi. Có 5! cách.
Giữa hai nam có khoảng trống. Xếp 4 nữ vào 4 trong 6 khoảng trống đó. Có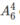 
cách.
Theo quy tắc nhân, có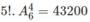 
cách.
18 tháng 5 2017
Để xác định, các ghế được đánh số thứ tự từ 1 đến 10 tính từ trái sang phải.
a) Nếu các bạn nam ngồi ở các ghế ghi số lẻ thì các bạn nữ ngồi ở các ghế còn lại. Có 5! cách xếp bạn nam, 5! cách xếp bạn nữ. Tất cả có \(\left(5!\right)^2\) cách xếp
Nếu bạn nam ngồi ở các ghế ghi số chẵn, các bạn nữ ngồi ở các ghế còn lại thì có \(\left(5!\right)^2\) cách xếp nam và nữ. Vậy có tất cả \(2.\left(5!\right)^2\) cách xếp nam nữ ngồi xen kẽ nhau.
b) Các bạn nam được bố trí ngồi ở các ghế từ \(k\) đến \(k+4,k=1,2,3,4,5,6\). Trong mỗi trường hợp có \(\left(5!\right)^2\) cách xếp nam và nữ. Vậy có \(6.\left(5!\right)^2\) cách xếp mà các bạn nam ngồi cạnh nhau.
Chọn C.
Ta coi 3 bạn nữ là vị trí thì số cách sắp xếp 6 là 6!, sau đó xếp 3 bạn nữ vào vị trí đó là 3! Nên số cách sắp xếp là 6!.3!