Cho z = a + b i , a , b ∈ R , z = 5 . Khi đó 3 a + 4 b lớn nhất khi
A. 25
B. 125
C. 45
D. 15
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 2 2019
Với 
Khi đó
Dấu bằng đạt tại
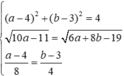
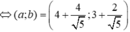
⇒ a - 2 b = - 2
Chọn đáp án B.
Mẹo trắc nghiệm: Có
Khi đó
Khi đó a-2b
Chọn đáp án B.
CM
10 tháng 1 2019
Đáp án A.
Gọi M x , y là điểm biểu diễn số phức z.
Từ giả thiết, ta có z − 4 − 3 i = 5 ⇔ x − 4 2 + y − 3 2 = 5 ⇒ M thuộc đường tròn (C) tâm I 4 ; 3 , bán kính R = 5 . Khi đó P = M A + M B , với A − 1 ; 3 , B 1 ; − 1 .
Ta có
P 2 = M A 2 + M B 2 + 2 M A . M B ≤ 2 M A 2 + M B 2 .
Gọi E 0 ; 1 là trung điểm của AB
⇒ M E 2 = M A 2 + M B 2 2 − A B 2 4 .
Do đó P 2 ≤ 4 M E 2 + A B 2 mà
M E ≤ C E = 3 5 s u y r a P 2 ≤ 4. 3 5 2 + 2 5 2 = 200.
Với C là giao điểm của đường thẳng EI
với đường tròn (C).
Vậy P ≤ 10 2 . Dấu “=” xảy ra
⇔ M A = M B M = C ⇒ M 6 ; 4 ⇒ a + b = 10.
CM
11 tháng 11 2017
Đáp án A
Gọi M(x;y) là điểm biều diễn số phức z.
Từ giả thiết, ta có |z - 4 - 3i| =
5
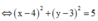
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R = 5
Khi đó P = MA + MB với A(-1;3), B(1;-1)
Ta có 
Gọi E(0;1) là trung điểm của AB 
Do đó 
mà 
suy ra 
Với C là giao điểm của đường thẳng EI với đường tròn (C)
Vậy 
Dấu “=”xảy ra 
CM
3 tháng 11 2018
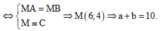
Đáp án A.
Gọi M(x;y) là điểm biểu diễn số phức z.
Từ giả thiết, ta có 
=> M thuộc đường tròn (C) tâm I(4;3), bán kính R = 5
Khi đó P = MA + MB, với A(-1;3), B(1;-1)
Ta có
Gọi E(0;1) là trung điểm của AB
Do đó 
mà 
suy ra 
Với C là giao điểm của đường thẳng EI với đường tròn (C).
Vậy 
Dấu “=” xảy ra 
=> a + b = 10
Đáp án B