Tia phân giác là gì
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VV
1
9 tháng 3 2018
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau
. Đường thẳng chứa tia phân giác gọi là đường phân giác.
5 tháng 9 2021
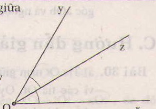
a: \(\widehat{a'Ob}+\widehat{aOb}=180^0\)
nên \(\widehat{a'Ob}=130^0\)
20 tháng 1 2018
ta có Ot là tia phân giác của góc mOn =>góc mOt = góc nOt = 120độ /2 =60độ
ta lại có góc OAK + góc AOK = 90 độ ( do tam giác AOK vuông ở K )
=> góc OAK = 30độ
góc AOH + góc OAH =90độ ( do tam giác AOH vuông tại H )
=> góc OAH = 30độ
Xét tam giác AOH và tam gics AOK ta có
góc OHA = góc OKA ( = 90 độ )
AO : cạnh chung )
góc AOH = góc AOK ( = 60 độ )
=> tam giác AOH = tam giác AOK ( cạnh huyền - góc nhọn )
=>góc HAO = góc KAO ( hai góc tương ứng )
=> OA là tia phân giác của góc KAH ( đpcm )
góc OAH + góc OAK = góc KAH => góc KAH = 30độ + 30độ = 60 độ
tam giác AOH = tam giác AOK => AH = AK
xét tam giác KAH ta có góc KAH = 60 độ
AK = AH
=> Tam giác KAH là tam giác đều
20 tháng 1 2018
Ta có góc tom = góc ton = 120°/2 = 60°( vì ot là tia p/g góc mon )
Xét ∆AOK và ∆AOH có
Góc AOH=góc AOK (cmt). (1)
Góc AHO= góc AKO= 90°. (2)
Từ (1),(2)=>góc HAO = góc KAO. (3)
=>∆AOK=∆AOH(g.g.g)
Từ (3) và OA nằm giữa OH,OK=>OA là tia p/g góc KAH
=> góc KAH=góc KAO*2=(180°-90°-60°)*2=30°*2=60°
Do ∆AHO=∆AKO=>AH=AK(2 cạnh tươg ứg) (4)
Từ (4)=> ∆AHK là ∆ cân tại A
4 tháng 1
Ta có: \(\widehat{ADE}=\widehat{CDE}=\dfrac{\widehat{ADC}}{2}\)(DE là phân giác của góc ADC)
\(\widehat{ABF}=\widehat{CBF}=\dfrac{\widehat{ABC}}{2}\)(BF là phân giác của góc ABC)
mà \(\widehat{ADC}=\widehat{ABC}\)(ABCD là hình bình hành)
nên \(\widehat{ADE}=\widehat{CDE}=\widehat{ABF}=\widehat{CBF}\)
Xét ΔADE và ΔCBF có
\(\widehat{EAD}=\widehat{FCB}\)(ABCD là hình bình hành)
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)(cmt)
Do đó: ΔADE=ΔCBF
=>AE=CF
Ta có: AE+EB=AB
CF+FD=CD
mà AE=CF và AB=CD
nên EB=FD
Ta có: AB//CD
E\(\in\)AB
F\(\in\)CD
Do đó: BE//DF
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau
Tia phân giác là tia nằm ở giữa 1 góc nào đó.
VD:góc xOy+Oyz=xOz.Tia Oy nằm giữa nên được gọi là tia phân giác
Hỉu chưa.