Trong các đường thẳng sau, đường thẳng nào là tiếp tuyến của đồ thị hàm số y = 2 x + 3 x + 2 chắn hai trục tọa độ một tam giác vuông cân
A. y = x + 2
B. y = x - 2
C. y = - x + 2
D. y = 1 4 x + 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=\dfrac{-4}{\left(x-1\right)^2}< 0\Rightarrow\) tiếp tuyến luôn có hệ số góc âm
Do tiếp tuyến tạo với trục tọa độ 1 tam giác vuông cân \(\Rightarrow\) nó có hệ số góc \(-1\)
Gọi tọa độ tiếp điểm là \(x_0\Rightarrow\dfrac{-4}{\left(x_0-1\right)^2}=-1\)
\(\Rightarrow\left(x_0-1\right)^2=4\Rightarrow\left[{}\begin{matrix}x_0=3\Rightarrow y_0=3\\x_0=-1\Rightarrow y_0=-1\end{matrix}\right.\)
Phương trình: \(\left[{}\begin{matrix}y=-\left(x-3\right)+3\\y=-\left(x+1\right)-1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=-x+6\\y=-x-2\end{matrix}\right.\)

a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.
Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.
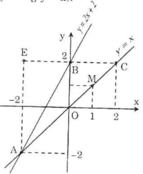
b) Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
2x + 2 = x
=> x = -2 => y = -2
Suy ra tọa độ giao điểm là A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
- Tọa độ điểm C:
Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
x = 2 => y = 2 => tọa độ C(2; 2)
- Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC)
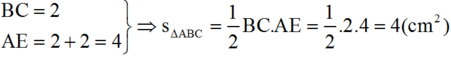
a)
+) y = 2x + 2
Cho x = 0 => y = 2
=> ( 0 ; 2 )
y = 0 => x = -1
=> ( -1 ; 0 )
- Đồ thị hàm số y = x đi qua 2 điểm có tọa độ ( 0 ; 0 )
- Đồ thị hàm số y = 2x + 2 đi qua 2 điểm có tọa độ ( 0 ; 2 ) và ( -1 ; 0 )
b) Hoành độ điểm A là nghiệm của PT sau :
x = 2x + 2
<=> 2x - x = -2
<=> x = -2
=> y = -2
Vậy A ( -2 ; -2 )
c) Tung độ điểm C = 2 => hoành độ điểm C là x = 2
=> C ( 2 ; 2 )
Từ A hạ \(AH\perp BC\), ta có : AH = 4cm
BC = 2cm
Vậy : ..............
\(\Rightarrow S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}.4.2=4\left(cm^2\right)\)

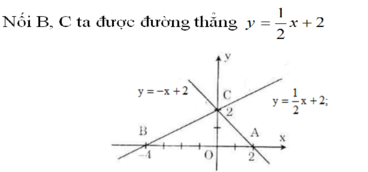
a) Vẽ đường thẳng y = -x + 2
Cho x = 0 => y = 2 được C(0; 2)
Cho y = 0 => x = 2 được A(2; 0)
Nối A, C ta được đường thẳng y = -x + 2
Cho x = 0 => y = 2 được C(0; 2)
Cho y = 0 => x = -4 được B(-4; 0)

c) Áp dụng định lí Pitago ta có:
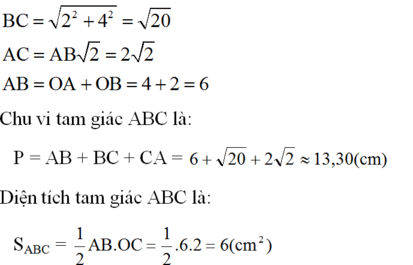

Đáp án D
Phương pháp:
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x o .
+) Tìm giao điểm của tiếp tuyến với các trục tọa độ.
+) Tính OA, OB, giải phương trình tìm x o → Phương trình tiếp tuyến và kết luận.

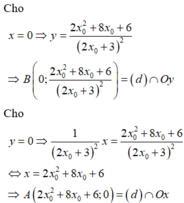
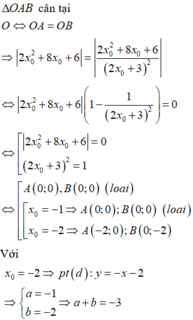
Đáp án là A