Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên
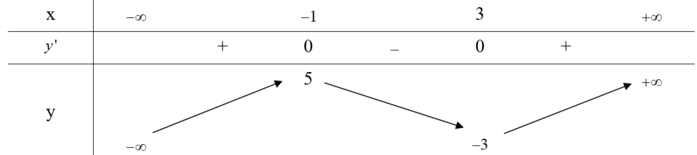
Phương trình f 1 − 2 x + 2 = 5 có tất cả bao nhiêu nghiệm thực phân biệt
A. 5
B. 4
C. 3
D. 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Kéo dài A’N, B’B, NP căt nhau tại H ta có :
S M B S = 1 2 . a 2 . a 4 . sin 60 o = 3 32 a 2 S A ' B ' N = 1 2 . a . a 2 . sin 60 0 = a 2 3 8 V H . A ' B ' N = 1 3 .2 a . S A ' B ' N = 1 3 .2 a . a 2 3 8 = 3 12 a 3 V H . M B P = 1 3 . a . S M B S = 1 3 . a . 3 32 a 2 = 3 96 . a 3 V M P B A ' B ' N = V H . A ' B ' N − V H . M B P = 7 3 96 a 3

Đáp án C
Dựa vào bảng biến thiên, phương trình f x = 2 m có đúng hai nghiệm phân biệt khi 2 m = 0 2 m < − 3 ⇔ m = 0 m < − 3 2

Đáp án C
Dựa vào bảng biến thiên, phương trình f x = 2 m có đúng hai nghiệm phân biệt khi 2 m = 0 2 m < − 3 ⇔ m = 0 m < − 3 2

Đáp án A
Để phương trình f(x)=m có 3 nghiệm phân biệt thì đường thẳng y=m cắt đồ thị hàm số tại 3 điểm phân biệt.
Dựa vào bảng biến thiên ta thấy -2<m<1

Đáp án D
Hàm số f(x) có dạng f ( x ) = ( x + 2 ) ( x - 1 ) 2 Giao với trục Oy tại (0, 2) .
=> 2<m<4.
Chọn phương án D.

Chọn B.
Đặt ![]()
Khi đó, phương trình f(
4
x
-
x
2
) =
log
2
m
trở thành ![]()
Để phương trình f( 4 x - x 2 ) = log 2 m có 4 nghiệm thực phân biệt thì đường thẳng y = log 2 m cắt đồ thị hàm số y = f(t) tại hai điểm phân biệt thỏa mãn t < 4.
Suy ra ![]()
Vậy m ∈ ( 1 2 ;8).
B
Đặt 1-2x=t với mỗi x ∈ ℝ có 1 và chỉ 1 giá trị t ∈ ℝ
Đồ thị của hàm số y = f(t) cũng là đồ thị của hàm số y = f(x)
Số nghiệm của phương trình (2) là số hoành độ giao
điểm của đồ thị hàm số y = f(t)với đường thẳng y = 3.
Có 3 giao điểm nên phương trình (2) có 3 nghiệm phân biệt.
Số nghiệm của phương trình (3) là số hoành độ giao điểm
của đồ thị hàm số y = f(t) với đường thẳng y = -7
Có 1 giao điểm nên phương trình (3) có đúng 1 nghiệm.
Nghiệm của phương trình (3) không trùng với nghiệm của
phương trình (2)
Vậy, phương trình có 4 nghiệm phân biệt