Cho F(x) là một nguyên hàm của hàm số f(x). Khi đó hiệu số F(1)-F(2) bằng
A. ∫ 1 2 f x d x
B. ∫ 1 2 - f x d x
C. ∫ 2 1 - F x d x
D. ∫ 1 2 - F x d x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

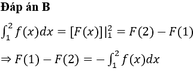

\(f\left(x\right)=\dfrac{x^2-1}{x^2}=1-\dfrac{1}{x^2}\)
\(\int f\left(x\right)dx=\int\left(1-\dfrac{1}{x^2}\right)dx=\int1dx-\int x^{-2}dx\)
=\(x-\dfrac{x^{-2+1}}{-2+1}+C=x-\dfrac{x^{-1}}{-1}+C=x+\dfrac{1}{x}+C\)
C=-1 ta được phương án A(ko tm câu hỏi)
C=0 ta được phương án B(ko tm câu hỏi)
C=2 ta được phương án C(ko tm câu hỏi)
=>chọn D

Chọn A
F ( x ) = ∫ 1 1 - 3 x + 1 d x = - 1 3 ∫ d ( 1 - 3 x ) 1 - 3 x + x = x - 2 3 1 - 3 x + C
F ( - 1 ) = 2 3 ⇒ C = 3 ⇒ F ( x ) = x - 2 3 1 - 3 x + 3

Ta có: f(-1) = 3.(-1)2 – 1 = 3.1- 1 = 2
f(-2) = 3.(-2)2 – 1 = 3.4 – 1 = 11
f(-3) = 3.(-3)2 – 1 = 3.9 – 1 = 26
f(0) = 3.02 - 1 = 0 - 1 = -1
Chọn (A).