Gọi x 1 , x 2 là hai nghiệm của phương trình 5 x - 1 5 . 0 , 2 x

PT

Pham Trong Bach

5 tháng 1 2019

Gọi x 1 , x 2 là hai nghiệm của phương trình 5 x - 1 + 5 . 0 , 2 x - = 26 . Tính S = x 1 2 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

5 tháng 1 2019

Đúng(0)

NT

nguyễn thị thúy an

12 tháng 6 2018 - olm

gọi x1; x2 là hai nghiệm của phương trình 5^(x-1)+5.0,2^(x-2)=26. Tính x1+x2

#Hỏi cộng đồng OLM #Toán lớp 9

1

AN

alibaba nguyễn

12 tháng 6 2018

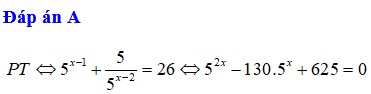
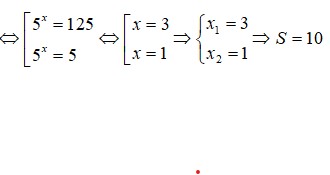
\(5^{x-1}+5.0,2^{x-2}=26\)

\(\Leftrightarrow5^{x-1}+\frac{5}{5^{x-2}}=26\)

\(\Leftrightarrow5^{x-1}+\frac{25}{5^{x-1}}=26\)

Đặt \(5^{x-1}=a\)

\(\Rightarrow a+\frac{25}{a}=26\)

\(\Leftrightarrow a^2-26a+25=0\)

\(\Leftrightarrow\orbr{\begin{cases}a=1\\a=25\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}5^{x-1}=1\\5^{x-1}=25\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x-1=2\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=3\end{cases}}\)

Đúng(0)

PT

Pham Trong Bach

19 tháng 12 2017

Gọi X là tập hợp các nghiệm nguyên chung của hai phương trình: ( x 2 − 9 ) . x 2 − ( 1 + 2 ) x + 2 = 0 (1) và ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 10

1

CM

Cao Minh Tâm

19 tháng 12 2017

Đáp án D

Đúng(0)

CP

Chi p

12 tháng 5 2023

Cho phương trình x2 + 5x − 4 = 0 . Gọi 1 2 x ; x là hai nghiệm của phương trình. Không
giải phương trinh, hăy tính giá trị biểu thức 2 2
1 2 1 2 Q = x + x + 6x x .

#Hỏi cộng đồng OLM #Toán lớp 9

1

2

2611

12 tháng 5 2023

Viết rõ đề bài ra bạn.

Đúng(0)

BV

Bi Vy

25 tháng 4 2021

Cho phương trình (lần x) x²-2(m-2) x+m² =0 (1) (m là tham số) 1: tìm m để phương trình (1) có nghiệm 2: Trong trường hợp phương trình (1) có nghiệm. Gọi x1, x2 là hai nghiệm của phương trình (1) a: dùng định lí Vi-Ét hãy tính x1+x2 và x1.x2 theo m b: tìm m để x1.x2-(x1+x2)-2=0

#Hỏi cộng đồng OLM #Toán lớp 9

0

LQ

Lê Quốc Huy

10 tháng 6 2017 - olm

Cho phương trình x² - 2x - 1 = 0. Gọi x₁,x₂ là các nghiệm của phương trình này.Hãy lập một phương trình bậc hai có hai nghiệm là số đối của x₁ và x₂

#Hỏi cộng đồng OLM #Toán lớp 9

3

LQ

Lê Quốc Huy

10 tháng 6 2017

ai gải giúp mìn với ạ

Đúng(0)

PP

Phạm Phú Sơn

26 tháng 3 2018

ko biết làm thông cảm :>

Đúng(0)

TT

Thanh Thảo

9 tháng 4 2017 - olm

Cho phương trình x² + 2mx – m -1 = 0

1)Chứng tỏ rằng với mọi giá trị của m, phương trình luôn có hai nghiệm phân biệt.

2) Gọi x₁, x₂ là hai nghiệm của phương trình. Tính x₁ + x₂ ; x₁ . x₂ theo m.

#Hỏi cộng đồng OLM #Toán lớp 9

2

PD

Phạm Đình Tiến

9 tháng 4 2017

(mình chỉ gợi ý cách làm thôi nhé!)

Phần 1 tính delta Cm delta luôn >0

Phần 2 Xử dụng hệ thức Vi-et

Đúng(0)

VN

Vũ Như Mai

10 tháng 4 2017

Câu b bạn học công thức là làm được mà. Câu a thì dùng \(\Delta\)như bạn kia nói ý

Đúng(0)

PT

Pham Trong Bach

28 tháng 12 2017

Cho hai phương trình: − 2 x 2 + 3 x + 5 = 0 (1) và 2 5 x − 1 x − 1 + 5 = 2 x (2)a) Chứng minh x ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

28 tháng 12 2017

a) b) HS tự làm.

c) Hai phương trình đã cho không tương đương.

Đúng(0)

CT

Camthe Thi

3 tháng 4 2020 - olm

1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>02/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -166/ Các nghiệm tự nhiên bé hơn 6 của...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 10

6

ND

Nguyễn Đức Anh

6 tháng 4 2020

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii

Đúng(0)

PM

Phạm Mạnh Hùng

7 tháng 4 2020

,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Đúng(0)

SH

Shimada Hayato

27 tháng 1 2023

Cho phương trình x²-2(m+1)x+2m-2=0 với x là ẩn số. Gọi hai nghiệm của phương trình là x₁, x₂, tính theo m thỏa mãn biểu thức x₁²+2(m+1)x₂+2m-2=9

#Hỏi cộng đồng OLM #Toán lớp 9

1

PV

Phạm Vĩnh Linh

27 tháng 1 2023

Theo định lý Vi-ét, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1.x_2=2m-2\end{matrix}\right.\)

Ta có: \(x_1^2+2\left(m+1\right)x_2+2m-2\)\(=x1^2+x_1+x_2.x_2+x_1.x_2\)

\(=x_1^2+2x_1x_2+x_2^2=\left(x_1+x_2\right)^2\) \(=\left[2\left(m+1\right)\right]^2=4\left(m+1\right)^2\)

Ta có: \(4\left(m+1\right)^2=9\Leftrightarrow\left(m+1\right)^2=\dfrac{9}{4}\) \(\Leftrightarrow\left[{}\begin{matrix}m+1=\dfrac{3}{2}\\m+1=\dfrac{-3}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=\dfrac{-5}{2}\end{matrix}\right.\)

Vậy \(m=\dfrac{1}{2};m=\dfrac{-5}{2}\) thoả mãn yêu cầu đề bài

Đúng(2)

PV

Phạm Vĩnh Linh

27 tháng 1 2023

Dấu bằng thứ nhất sau chữ ta có đầu tiên sửa thành: \(x_1^2+\left(x_1+x_2\right).x_2+x_1x_2\)

Đúng(0)

MT

Mè Thị Thu Hà

12 tháng 5 2015 - olm

Cho phương trình x²- 2(m - 1)x + m² - 4m + 5 = 0 (1)

a) Giải phương trình khi m=4

b) Tìm giá trị của m để phương trình (1) có ghiệm

c) Gọi x₁, x₂ là hai nghiệm của phương trình (1). Hãy tìm giá trị nhỏ nhát của biểu thức M = x₁x₂ - 2(x₁ + x₂)

#Hỏi cộng đồng OLM #Toán lớp 9

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP