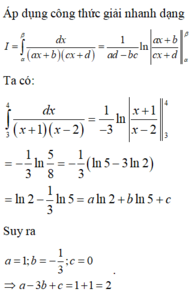Biết ∫ 1 2 x 3 d x x 2 1 - 1 = a 5 b 2 c với a, b, c là các số hữu...

PT

Pham Trong Bach

23 tháng 9 2019

Biết ∫ 1 2 x 3 d x x 2 + 1 - 1 = a 5 + b 2 + c với a, b, c là các số hữu...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

23 tháng 9 2019

Đúng(0)

NT

Nguyễn Thu Phương

27 tháng 2 2022

6.Tìm x. biết: x-7/2 = -3/4 A.-43/20 B.43/20 C.13/20 D.-13/207. Tìm x, biết: 1/3+x=5/6A.3/4 B.-3/4 C.1/2 D.1/68. Tìm số hữu ti x, biết: 1/4x:2/5=5/6A.-4 B.4/3 C.-4/3 D.3/49. Đổi hỗn số sau thành phân số: 4 và 2/5 A.8/5 B.22/5 C.6/5 D.2/5 10. Rút gọn phân số sau về số tối giản: -48/64 A. 3/4 B.4/3 C.-4/3 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 6

2

NL

Nguyễn Lê Phước Thịnh

27 tháng 2 2022

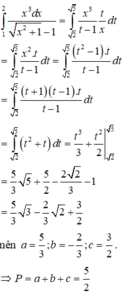
Câu 6: Khôg có cau nào đúng

Câu 7: C

Câu 8: B

Câu 9: B

Câu 10: D

Đúng(1)

D

Dark_Hole

27 tháng 2 2022

6Không có đáp án nào đúng x=11/4

7C

8B

9B

10D

Đúng(1)

NM

Nguyễn Minh

16 tháng 6 2019 - olm

1.Tìm các số nguyên dương a,b thỏa 1/a+1/b=1/p với p là số nguyên tố2.Cho các số nguyên dương a<bc<d<e<f . Chứng minh a+c+e/a+b+c+d+e+f <1/23.Với giá trị nào của a thuộc Z thì số hữu tỉ x là số dương ? Là số âm ? Là số không âm ? Là số không dương ? Không là số dương cũng ko là số âm ?Câu a .x=2a+7/-5Câu b. x=a-4/a^2 Câu c.. x=a^2+9/-7Câu d. x=a-6/a-11Các bạn giải hộ mình nhé . Mik càn gấp ....

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

3

D

Darlingg🥝

16 tháng 6 2019

Một họ gồm m phần tử đại diện cho m lớp tương đương nói trên được gọi là một hệ thặng dư đầy đủ modulo m. Nói cách khác, hệ thặng dư đầy đủ modulo m là tập hợp gồm m số nguyên đôi một không đồng dư với nhau theo môđun m.

(x₁, x₂, …, x_m) là hệ thặng dư đầy đủ modulo m ó x_i – x_j không chia hết cho m với mọi 1 £ i < j £ m.

Ví dụ với m = 5 thì (0, 1, 2, 3, 4), (4, 5, 6, 7, 8), (0, 3, 6, 9, 12) là các hệ thặng dư đầy đủ modulo 5.

Từ định nghĩa trên, ta dễ dàng suy ra tính chất đơn giản nhưng rất quan trọng sau:

Tính chất 1: Nếu (x₁, x₂, …, x_m) là một hệ thặng dư đầy đủ modulo m thì

a) Với a là số nguyên bất kỳ (x₁+a, x₂+a, …, x_m+a) cũng là một hệ thặng dư đầy đủ modulo m.

b) Nếu (a, m) = 1 thì (ax₁, ax₂, …, ax_m) cũng là một hệ thặng dư đầy đủ modulo m.

Với số nguyên dương m > 1, gọi j(m) là số các số nguyên dương nhỏ hơn m và nguyên tố cùng nhau với m. Khi đó, từ một hệ thặng dư đầy đủ mô-đun m, có đúng j(m) phần tử nguyên tố cùng nhau với m. Ta nói các phần tử này lập thành một hệ thặng dư thu gọn modulo m. Nói cách khác

(x₁, x₂, …, x_j(m)) là hệ thặng dư thu gọn modulo m ó (x_i, m) = 1 và x_i – x_j không chia hết cho m với mọi 1 £ i < j £ j(m).

Ta có

Tính chất 2: (x₁, x₂, …, x_j(m)) là hệ thặng dư thu gọn modulo m và (a, m) = 1 thì

(ax₁,a x₂, …, ax_j(m)) cũng là một hệ thặng dư thu gọn modulo m.

Định lý Wilson. Số nguyên dương p > 1 là số nguyên tố khi và chỉ khi (p-1)! + 1 chia hết cho p.

Chứng minh. Nếu p là hợp số, p = s.t với s, t > 1 thì s £ p-1. Suy ra (p-1)! chia hết cho s, suy ra (p-1)! + 1 không chia hết cho s, từ đó (p-1)! + 1 không chia hết cho p. Vậy nếu (p-1)! + 1 chia hết cho p thì p phải là số nguyên tố.

~Hok tốt`

P/s:Ko chắc

Đúng(0)

ZC

zZz Cool Kid_new zZz

17 tháng 6 2019

\(a< b< c< d< e< f\)

\(\Rightarrow a+c+e< b+d+f\)

\(\Rightarrow2\left(a+c+e\right)< a+b+c+d+e+f\)

\(\Rightarrow\frac{a+c+e}{a+b+c+d+e+f}< \frac{1}{2}\)

Đúng(0)

PT

Pham Trong Bach

29 tháng 3 2017

Biết ∫ 3 4 d x ( x + 1 ) ( x - 2 ) = a ln 2 + b ln 5 + c ,...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

29 tháng 3 2017

Đáp án B

Đúng(0)

PT

Pham Trong Bach

22 tháng 9 2018

Biết ∫ 3 4 d x ( x + 1 ) ( x - 2 ) = a ln 2 + b ln 5 + c với a, b, c là các số hữu tỉ.Tính S = a – 3b...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

22 tháng 9 2018

Đúng(0)

VT

vu tuan anh

4 tháng 3 2021 - olm

Câu hỏi 2 : Vì sao các số 1,2 ; -1,75 ; 0 ; 6 : là những số hữu tỉ ? Câu hỏi 3 : Số nguyên a có phải là số hữu tỉ không ? Vì sao ? Câu hỏi 4 : Trình bày cách biểu diễn một số hữu tỉ trên trục số . Câu hỏi 5 : Trình bày các bước thực hiện để so sánh hai số hữu tỉ x và y . Câu hỏi 6 : Trình bày các bước thực hiện để chỉ ra được dạng tổng quát của hữu tỉ X. Câu hỏi 7 : Nêu định...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

0

DL

Dũng Lương Trí

9 tháng 1 2019 - olm

Câu 1 : Tìm x , biết :

\(|x^2+|x+1||\)=x²+ 5

Câu 2 :

a) Tìm số hữu tỉ x,y với x,y khác 0 , thỏa mãn : x+y=x.y=x:y

b)Cho 4 số tự nhiên a,b,c,d khác 0 thỏa mãn : a²+b²=c²+d² . Chứng minh : a+b+c+d là hợp số

#Hỏi cộng đồng OLM #Toán lớp 7

1

SP

Siêu Phẩm Hacker

9 tháng 1 2019

Câu 1 .

\(\left|x^2+|x+1|\right|=x^2+5\)

\(Đkxđ:x^2+5\ge0\)

\(\Leftrightarrow x^2\ge-5,\forall x\) ( với mọi x , vì bất cứ số nào bình phương cũng lớn hơn hoặc bằng - 5 )

\(\Leftrightarrow\hept{\begin{cases}x^2+\left|x+1\right|=x^2+5\\x^2+\left|x+1\right|=-x^2-5\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}\left|x+1\right|=5\\\left|x+1\right|=-2x^2-5\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x+1=5;x+1=-5\\x+1=-2x^2-5;x+1=2x^2+5\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x=4;x=-6\\2x^2+x+1=0;-2x^2+x-4=0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x=4;x=-6\\2x^2+x+1=0\left(VN\right);-2x^2+x-4=0\left(VN\right)\end{cases}}\) ( VN là vô nghiệm nha )

Vậy : x = 4 hoặc x = -6

Đúng(0)

LN

Lê Ngọc Hà

16 tháng 10 2020 - olm

Tìm số hữu tỉ x biết

a) 2/3.x-2/5=1/2.x-1/3

b) 1/3.x+2/5(x+1)=0

c) 2/3-1/3(x-3/2)-1/2(2x+1)=5

d) 11/5-(7/9-x).3/8=61/90+x/3

#Hỏi cộng đồng OLM #Toán lớp 7

1

HQ

Huỳnh Quang Sang

17 tháng 10 2020

a) \(\frac{2}{3}x-\frac{2}{5}=\frac{1}{2}x-\frac{1}{3}\)

=> \(\frac{2}{3}x-\frac{2}{5}-\frac{1}{2}x+\frac{1}{3}=0\)

=> \(\left(\frac{2}{3}x-\frac{1}{2}x\right)+\left(-\frac{2}{5}+\frac{1}{3}\right)=0\)

=> \(\frac{1}{6}x-\frac{1}{15}=0\Rightarrow\frac{1}{6}x=\frac{1}{15}\Rightarrow x=\frac{1}{15}:\frac{1}{6}=\frac{1}{15}\cdot6=\frac{2}{5}\)

Vậy x = 2/5

b) \(\frac{1}{3}x+\frac{2}{5}\left(x+1\right)=0\)

=> \(\frac{1}{3}x+\frac{2}{5}x+\frac{2}{5}=0\)

=> \(\frac{11}{15}x+\frac{2}{5}=0\Rightarrow\frac{11}{15}x=-\frac{2}{5}\)

=> \(x=\left(-\frac{2}{5}\right):\frac{11}{15}=\left(-\frac{2}{5}\right)\cdot\frac{15}{11}=-\frac{6}{11}\)

Vậy x = -6/11

c) \(\frac{2}{3}-\frac{1}{3}\left(x-\frac{3}{2}\right)-\frac{1}{2}\left(2x+1\right)=5\)

=> \(\frac{2}{3}-\frac{1}{3}x+\frac{1}{2}-x-\frac{1}{2}=5\)

=> \(\left(\frac{2}{3}+\frac{1}{2}-\frac{1}{2}\right)+\left(-\frac{1}{3}x-x\right)=5\)

=> \(\frac{2}{3}-\frac{4}{3}x=5\)

=> \(\frac{4}{3}x=-\frac{13}{3}\Rightarrow x=\left(-\frac{13}{3}\right):\frac{4}{3}=\left(-\frac{13}{3}\right)\cdot\frac{3}{4}=-\frac{13}{4}\)

Vậy x = -13/4

d) \(\frac{11}{5}-\left(\frac{7}{9}-x\right)\cdot\frac{3}{8}=\frac{61}{90}+\frac{x}{3}\)

=> \(\frac{11}{5}-\frac{3}{8}\left(\frac{7}{9}-x\right)=\frac{61}{90}+\frac{30x}{90}\)

=> \(\frac{11}{5}-\frac{7}{24}+\frac{3}{8}x=\frac{61+30x}{90}\)

=> \(\frac{229}{120}+\frac{3}{8}x=\frac{61+30x}{90}\)

=> \(\frac{229}{120}+\frac{3x}{8}=\frac{61+30x}{90}\)

=> \(\frac{229}{120}+\frac{45x}{120}=\frac{61+30x}{90}\)

=> \(\frac{229+45x}{120}=\frac{61+30x}{90}\)

=> \(\frac{3\left(229+45x\right)}{360}=\frac{4\left(61+30x\right)}{360}\)

=> \(3\left(229+45x\right)=4\left(61+30x\right)\)

=> \(687+135x=244+120x\)

=> \(687+135x-244-120x=0\)

=> \(\left(687-244\right)+\left(135x-120x\right)=0\)

=> \(443+15x=0\)

=> \(15x=-443\Rightarrow x=-\frac{443}{15}\)

Vậy x = -443/15

Đúng(0)

LT

lucky tomato

30 tháng 3 2020 - olm

TÌM CÁC SỐ HỮU TỈ a,b,c BIẾT
\(\frac{x^3}{x^4-1}=\frac{a}{x-1}+\frac{b}{x+1}+\frac{cx+d}{x^2+1}\)

#Hỏi cộng đồng OLM #Toán lớp 8

2

NH

Nguyễn Hoàng Oanh

1 tháng 4 2020

\({ x^3\over x^4-1 }={{ a(x+1)+b(x-1)}\over{x^2-1}} +{{cx+d}\over{x^2+1}}\)=\({(ax+a+bx-b)(x^2 +1) +(cx+d) (x^2-1)}\over{x^4-1}\) =\({ax^3 +ax^2+bx^3-bx^2+ax+a+bx-b +cx^3 +dx^2-cx-d}\over{x^4-1} \) Suy ra \(x^3=ax^3 +ax^2+bx^3-bx^2+ax+a+bx-b +cx^3 +dx^2-cx-d \) \(= x^3(a+b+c)+x^2(a-b+d)+x(a+b-c)+(a-b-d)\) Điều này chỉ xảy ra khi đồng thời : a+b+c=1; a-b+d=0; a+b-c=0; a-b-d=0 khi và chỉ khi a=0,25 ; b=0,25 ; c=0,5 ; d=0

Vậy .......

Đúng(0)

S

✰๖ۣۜŠɦαɗøω✰

1 tháng 4 2020

Biến đổi đẳng thức về dạng :

\(\frac{x^3}{x^4-1}=\frac{\left(a+b+c\right).x^3+\left(a-b+d\right).x^2+\left(a+b-c\right).x+\left(a-b-d\right)}{x^4-1}\)

Suy ra \(\hept{\begin{cases}a+b+c=1\\a-b+d=0\\a+b-c=0\end{cases}}\)Giải ra ta được a=b=1/4 ; c = 1/2 ; d = 0

\(\hept{a-b-d=0}\)

( Lưu ý : Phần lưu ý này không cần phải ghi : Nối dấu ngoặc 3 ý và dấu ngoặc 1 ý làm 1 )

Đúng(0)

TT

Tae Tae

28 tháng 6 2019 - olm

1 ) Tìm X :

a) 2 . ( 3/4 - 5x ) = 4/5 - 3x

b) 3/2 - 4 ( 1/4 - x ) = 2/3 - 7x

2) Tìm điều kiện của tử và mẫu để các số hữu tỉ sau thỏa mãn :

a) 2 / x-1 là só hữu tỉ âm

b) -5 / x-1 là số hữu tỉ âm

c) 7 / x-6 là số hữu tr dương

#Hỏi cộng đồng OLM #Toán lớp 7

3

PT

Phạm Thị Thùy Linh

28 tháng 6 2019

Câu 1 :

\(a,2\left(\frac{3}{4}-5x\right)=\frac{4}{5}-3x\)

\(\Rightarrow\frac{3}{2}-10x=\frac{4}{5}-3x\)

\(\Rightarrow7x=\frac{3}{2}-\frac{4}{5}\)

\(\Rightarrow7x=\frac{7}{10}\)\(\Leftrightarrow x=0,1\)

\(b,\frac{3}{2}-4\left(\frac{1}{4}-x\right)=\frac{2}{3}-7x\)

\(\Rightarrow\frac{3}{2}-1+4x=\frac{2}{3}-7x\)

\(\Rightarrow11x=\frac{2}{3}+1-\frac{3}{2}\)

\(\Rightarrow11x=\frac{4+6-9}{6}-\frac{1}{6}\)

\(\Rightarrow x=\frac{1}{66}\)

Đúng(1)

PT

Phạm Thị Thùy Linh

28 tháng 6 2019

Câu 2 :

\(a,\frac{2}{x-1}< 0\)

Vì \(2>0\Rightarrow\)để \(\frac{2}{x-1}< 0\)thì \(x-1< 0\Leftrightarrow x< 1\)

\(b,\frac{-5}{x-1}< 0\)

Vì \(-5< 0\)\(\Rightarrow\)để \(\frac{-5}{x-1}< 0\)thì \(x-1>0\Rightarrow x>1\)

\(c,\frac{7}{x-6}>0\)

Vì \(7>0\Rightarrow\)để \(\frac{7}{x-6}>0\)thì \(x-6>0\Rightarrow x>6\)

Đúng(0)

TP

tam phung

23 tháng 1 2020 - olm

cho f(x)=ax^3+bx^2+cx+d với a b c d là các số hữu tỉ biết 7a +5b +c + 2d = 0 cm F(-1).F(2) \(\le\) 0

#Hỏi cộng đồng OLM #Toán lớp 7

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP