Cho số phức z=a+bi (a,b ) và xét hai số phức . Trong các khẳng định dưới đây, khẳng định nào đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Phương pháp:
Từ ![]() tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z=x+yi
tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z=x+yi
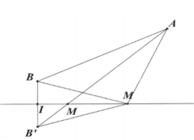
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
![]() nhỏ nhất
nhỏ nhất
![]()
Cách giải: Gọi z=x+ui ta có:
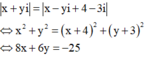
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
![]() nhỏ nhất.
nhỏ nhất.
Ta có: ![]()
Dấu bằng xảy ra ![]()
![]() M thuộc trung trực của AB.
M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có ![]()
Phương trình đường trung trực của AB là
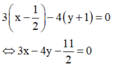
Để ![]()
![]() Tọa độ điểm M là nghiệm của hệ phương trình
Tọa độ điểm M là nghiệm của hệ phương trình


Đáp án C
- Nhìn vào hình vẽ ta có phần thực a bị giới hạn − 2 < a < 2 , b ∈ ℝ
Chú ý: Cho số phức z = a + bi, điểm M(a;b) trong hệ trục tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z.

Đáp án D.
Đặt z = a + bi => a + bi ![]()
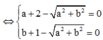
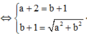
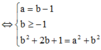

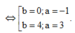
Do |z| > 1 => a = 3, b = 4
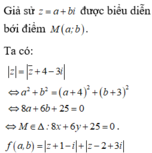
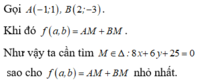


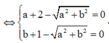
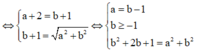
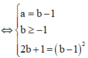
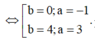
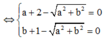
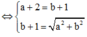
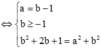
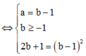
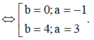

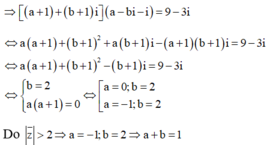
ĐÁP ÁN: A