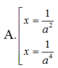
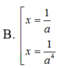
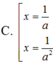
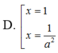
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
tham khảo.
Đồ thị của hai hàm số \(y=\log_ax\) và \(y=b\) luôn cắt nhau tại một điểm duy nhất. Khi đó phương trình \(\log_ax=b\) có nghiệm duy nhất \(x=a^b\).
a, ĐK: \(4x+4>0\Rightarrow x>-1\)
\(log_6\left(4x+4\right)=2\\ \Leftrightarrow4x+4=36\\ \Leftrightarrow4x=32\\ \Leftrightarrow x=8\left(tm\right)\)
Vậy x = 8.
b, ĐK: \(x-2>0\Rightarrow x>2\)
\(log_3x-log_3\left(x-2\right)=1\\ \Leftrightarrow log_3\left(x^2-2x\right)=1\\ \Leftrightarrow x^2-2x-3=0\\ \Leftrightarrow\left(x-3\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy x = 3.
\(a,\left(\dfrac{1}{4}\right)^{x-2}=\sqrt{8}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{2x-4}=\left(\dfrac{1}{2}\right)^{-\dfrac{3}{2}}\\ \Leftrightarrow2x-4=-\dfrac{3}{2}\\ \Leftrightarrow2x=\dfrac{5}{2}\\ \Leftrightarrow x=\dfrac{5}{4}\)
\(b,9^{2x-1}=81\cdot27^x\\ \Leftrightarrow3^{4x-2}=3^{4+3x}\\ \Leftrightarrow4x-2=4+3x\\ \Leftrightarrow x=6\)
c, ĐK: \(x-2>0\Rightarrow x>2\)
\(2log_5\left(x-2\right)=log_59\\
\Leftrightarrow log_5\left(x-2\right)^2=log_59\\
\Leftrightarrow\left(x-2\right)^2=3^2\\
\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm là x = 5.
d, ĐK: \(x-1>0\Leftrightarrow x>1\)
\(log_2\left(3x+1\right)=2-log_2\left(x-1\right)\\ \Leftrightarrow log_2\left(3x+1\right)\left(x-1\right)=2\\ \Leftrightarrow3x^2-2x-1=4\\ \Leftrightarrow3x^2-2x-5=0\\ \Leftrightarrow\left(3x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm \(x=\dfrac{5}{3}\)
tham khảo
a)Điều kiện \(3-x>0\) hay \(x< 3\)
\(4-log\left(3-x\right)=3log\left(3-x\right)=1\Leftrightarrow10^1=3-x\)
Vậy nghiệm của phương trình là \(x=2\) thỏa mãn điều kiện
b) Điều kiện \(x+2>0\) và \(x-1>0\) tức là \(x>1\)
\(\left(x+2\right)\left(x-1\right)=2\Rightarrow x^2+x-4=0\)
Vậy pt có nghiệm \(x=\dfrac{-1+\sqrt{17}}{2}\)
\(a,3^{1-2x}=4^x\\ \Leftrightarrow1-2x=log_34^x\\ \Leftrightarrow1-2x=xlog_34\\ \Leftrightarrow2x+xlog_34=1\\ \Leftrightarrow x\left(2+log_34\right)=1\\ \Leftrightarrow x=\dfrac{1}{2+log_34}=\dfrac{1}{log_39+log_34}=\dfrac{1}{log_336}=log_{36}3\)
b, ĐK: \(x>-1\)
\(log_3\left(x+1\right)+log_3\left(x+4\right)=2\\ \Leftrightarrow log_3\left(x^2+5x+4\right)=2\\ \Leftrightarrow x^2+5x+4=9\\ \Leftrightarrow x^2+5x-5=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-5+3\sqrt{5}}{2}\left(tm\right)\\x=\dfrac{-5-3\sqrt{5}}{2}\left(ktm\right)\end{matrix}\right.\)
Chọn C