Cho (P): (m+1)x+(1-2m)y+(m-1)z-(m+2)=0 ( tham số m ∈ ℝ ) thì

![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Ta có y ' = 3 ( m - 1 ) + ( 2 m + 1 ) sin x để hàm số nghịch biến trên ℝ thì y ' ≤ 0 với mọi x xét BPT
3 ( m - 1 ) + ( 2 m + 1 ) sin x ≤ 0 Nếu m = - 1 2 BPT luôn đúng. Với m > - 1 2 BPT ⇔ sin x ≤ 3 ( 1 - m ) 2 m + 1 để hàm số luôn nghịch biến với mọi x thì 3 ( 1 - m ) 2 m + 1 ≥ 1 ⇒ - 1 2 < m ≤ 2 5 . Với m < - 1 2 BPT ⇔ sin x ≥ 3 ( 1 - m ) 2 m + 1 để hàm số luôn nghịch biến với mọi x thì 3 ( 1 - m ) 2 m + 1 ≤ - 1 ⇒ m < - 1 2
Kết hợp hai trường hợp ta có m ≤ 2 5

Chọn A
Tập xác định: D =
ℝ
. Ta có ![]() Để hàm số nghịch biến trên
ℝ
thì
Để hàm số nghịch biến trên
ℝ
thì
![]()
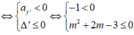
![]()

Đáp án B
Ta có n P → = (m2 - 2m; 1; m - 1). Mặt phẳng (P) song song với trục Ox khi và chỉ khi
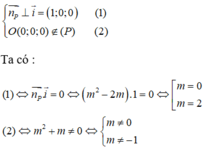
Từ đó ta được m=2.
Vậy đáp án B là đáp án đúng.

Đáp án B
Ta có n p → = (1; m 2 - 2m; m - 1). Mặt phẳng (P) song song với trục Oy khi và chỉ khi
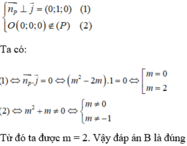

Ta co:\(\Sigma\frac{x\left(yz+1\right)^2}{z^2\left(zx+1\right)}=\Sigma\frac{\left(y+\frac{1}{z}\right)^2}{z+\frac{1}{x}}\ge\frac{\left(x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2}{x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}=x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\)Ta lai co:
\(\Sigma x+\Sigma\frac{1}{x}=\Sigma\left(x+\frac{1}{4x}\right)+\frac{3}{4}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\ge3+\frac{3}{4}.\frac{9}{x+y+z}\ge3+\frac{3}{4}.\frac{9}{\frac{3}{2}}=\frac{15}{2}\)
Dau '=' xay ra khi \(x=y=z=\frac{1}{2}\)
Vay \(P_{min}=\frac{15}{2}\)khi \(x=y=z=\frac{1}{2}\)
Chọn B