Cho hình lăng trụ ABC.A'B'C', M là trung điểm của CC'. Mặt phẳng (ABM) chia khối lăng trụ thành hai khối đa diện. Gọi V 1 là thể tích khối đa diện chứa đỉnh C và V 2 là thể tích khối đa diện còn lại. Tính tỉ số V 1 V 2 .
![]()
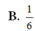
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
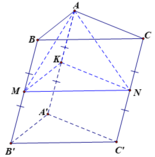
Gọi K là trung điểm của AA' và V, VABC.KMN, VA.KMN lần lượt là thể tích khối lăng trụ ABC. A'B'C' khối lăng trụ ABC. KMN và thể tích khối chóp A. MNK. Khi đó
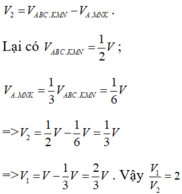

Đáp án B.
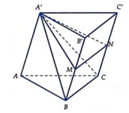
Vì M,N lần lượt là trung điểm của BB' và CC' nên ta có:
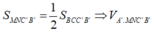
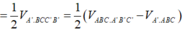
Lại có:
![]()

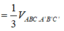
Vậy tỉ số
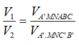
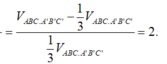

Đáp án B
Vì M,N lần lượt là trung điểm của BB' và CC' nên ta có:
S M N C ' B ' = 1 2 S B C C ' B ' ⇒ V A ' . M N C ' B ' = 1 2 V A ' . B C C ' B ' = 1 2 V A B C . A ' B ' C ' - V A ' . A B C
Lại có:
V A ' . A B C = 1 3 V A B C . A ' B ' C ' ⇒ V A ' . M N C ' B ' = 1 2 V A B C . A ' B ' C ' - 1 3 V A B C . A ' B ' C ' = 1 3 V A B C . A ' B ' C '
Vậy tỉ số V 1 V 2 = V A ' M N A B C V A ' . M N C ' B ' = V A B C . A ' B ' C ' - 1 3 V A B C . A ' B ' C ' 1 3 V A B C . A ' B ' C ' = 2