Các giá trị thực của x thỏa mãn điều kiện
3
x
<
27
là ...
Đọc tiếp
Các giá trị thực của x thỏa mãn điều kiện 3 x < 27 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu 
CM
1 tháng 3 2018
Đáp án C
Phương pháp:
Rút y theo x từ phương trình (1), thế vào phương trình (2) để tìm khoảng giá trị của x.
Đưa biểu thức P về 1 ẩn x và tìm GTLN, GTNN của biểu thức P.
Cách giải: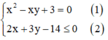 
Ta nhận thấy x = 0 không thỏa mãn phương trình (1), do đó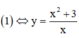 
thế vào (2):
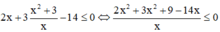
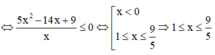
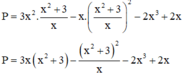
Sử dụng MTCT ta tính được
TH
1
DT
30 tháng 4 2021
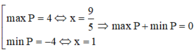
x + y = 1 => y = 1 - x
A = x3 + y3 = (x + y)(x2 - xy + y2)
= x2 - x(1 - x) + (1 - x)2
= x2 - x + x2 + x2 - 2x + 1
= 3x2 - 3x + 1
= 3(x2 - x + \(\dfrac{1}{3}\))
= 3(x2 - 2x.\(\dfrac{1}{2}\) + \(\dfrac{1}{4}+\dfrac{1}{12}\))
= 3(x - \(\dfrac{1}{2}\))2 + \(\dfrac{1}{4}\) ≥ \(\dfrac{1}{4}\) ∀x
Dấu "=" xảy ra ⇔ x - \(\dfrac{1}{2}\) = 0 ⇔ x = \(\dfrac{1}{2}\)
Vậy minA = \(\dfrac{1}{4}\) ⇔ x = \(\dfrac{1}{2}\)
CM
27 tháng 3 2019
Đáp án B.
Từ giả thiết, suy ra 5 x + 2 y + 1 3 x y - 1 + x + 1 = 5 x y - 1 + 1 3 x + 2 y + x y - 2 y
⇔ 5 x + 2 y - 1 3 x + 2 y + x + 2 y = 5 x y - 1 - 1 3 x y - 1 + ( x y - 1 ) (1)
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 + ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f (t) luôn đồng biến trên ℝ .
Suy ra 1 ⇔ f ( x + 2 y ) = f ( x y - 1 ) ⇔ x + 2 y = x y - 1 ⇔ x + 1 = y ( x - 2 )
y = x + 1 x - 2
Do y > 0 nên x + 1 x - 2 > 0 ⇔ x > 2 x < - 1 . Mà x > 0 nên x > 2.
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm g ' ( x ) = 1 - 3 x - 2 2 > 0 , g ' ( x ) = 0 ⇔ ( x - 2 ) 2 = 3
⇔ x = 2 + 3 ( t m ) x = 2 - 3 ( L ) . Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy m i n g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và y = 1 + 3 .
CM
22 tháng 1 2018
Từ giả thiết ta suy ra
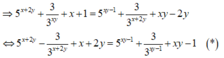
Xét hàm số f ( t ) = 5 t - 1 3 t + t với t ∈ ℝ , f ' ( t ) = 5 t . ln 5 + 3 - t . ln 3 + 1 > 0 ; ∀ t ∈ ℝ
Suy ra y= f( t) là hàm số đồng biến trên R mà từ ( * ) suy ra
f (x+ 2y) =f( xy-1) hay x+ 2y= xy-1
với x>0 suy ra y>1.
Khi đó
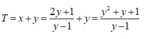
Xét hàm số
f ( y ) = y 2 + y + 1 y - 1 t r ê n 1 ; + ∞ f ' y = y 2 - 2 y - 2 y - 1 2 = 0 ⇔ y = ± 1 + 3 f 1 + 3 = 3 + 2 3 ; lim y → 1 f ( y ) = lim y → + ∞ f ( y ) = + ∞
Do đó, giá trị nhỏ nhất của hàm số là 3 + 2 3 .
Vậy kết quả là 3 + 2 3
Chọn B.
CM
26 tháng 4 2018
Đáp án B.
Từ giả thiết, suy ra
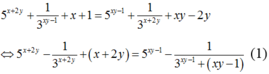
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
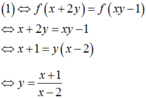
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
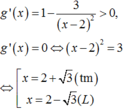
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2021
Do \(x^2+y^2=1\), đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\)
\(P=\left(3-sina\right)\left(3-cosa\right)=9-3\left(sina+cosa\right)+sina.cosa\)
Đặt \(sina+cosa=t\Rightarrow t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(t^2=1+2sina.cosa\Rightarrow sina.cosa=\dfrac{t^2-1}{2}\)
\(P=9-3t+\dfrac{t^2-1}{2}=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\)
Xét hàm \(f\left(t\right)=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\) trên \(\left[-\sqrt{2};\sqrt{2}\right]\)
\(f'\left(t\right)=t-3=0\Rightarrow t=3\notin\left[-\sqrt{2};\sqrt{2}\right]\)
\(f\left(-\sqrt{2}\right)=\dfrac{19+6\sqrt{2}}{2}\) ; \(f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\)
\(\Rightarrow P_{min}=f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\) khi \(t=\sqrt{2}\)
Chọn C