Trong không gian Oxyz, cho hai đường thẳng , và mặt phẳng (P): x +2y +3z -5 =0. Đường thẳng vuông góc với (P), cắt cả có phương trình là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình \(d_1\) : \(\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{-1}\) dạng tham số: \(\left\{{}\begin{matrix}x=1+t\\t=2-t\\z=3-t\end{matrix}\right.\)
Gọi A là giao điểm d1 và (P), tọa độ A thỏa mãn:
\(3-t-1=0\Rightarrow t=2\Rightarrow A\left(3;0;1\right)\)
\(\overrightarrow{n_P}=\left(0;0;1\right)\) ; \(\overrightarrow{n_Q}=\left(1;1;1\right)\)
\(\overrightarrow{u_{\Delta}}=\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(-1;1;0\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{n_P}\right]=\left(1;1;0\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=3+t\\y=t\\z=1\end{matrix}\right.\)

Đáp án A.
Đường thẳng d qua điểm M(2;-2;1) và có vectơ chỉ phương u → = ( - 3 ; 1 ; - 2 )
Đường thẳng d' qua điểm N(0;4;2) và có vectơ chỉ phương u ' → = 6 ; - 2 ; 4
Ta có
-
3
6
=
1
-
2
=
-
2
4
nếu
u
→
,
u
'
→
cùng phương. Lại có
M
2
;
-
2
;
-
1
![]()
Vậy d ∥ d '

Đáp án D.
Ta dễ thấy hai đường thẳng d và d ' song song.
Hai đường thẳng d và d ' lần lượt đi qua hai điểm M 5 ; 1 ; 5 và N 3 ; − 3 ; 1 và có vtcp u → = 2 ; − 1 ; 1 . Ta có M N → = − 2 ; − 4 ; − 4 .
Hai vecto M N → và u → không cùng phương và có giá nằm trên mặt phẳng P nên ta có vtpt của mặt phẳng P là n → = M N → ; u → .
Ta tìm tọa độ của n → bằng MTCT:

⇒ n → = − 8 ; − 6 ; 10
Mặt phẳng P có vtpt n → = − 8 ; − 6 ; 10 và đi qua M 5 ; 1 ; 5 nên có phương trình P : − 8 x − 5 − 6 y − 1 + 10 z − 5 = 0 ⇔ P : 4 x + 3 y − 5 z + 2 = 0 .Ta chọn D.

Chọn B
Gọi (P) là mặt phẳng chứa hai đường thẳng d₁ và d₂
Khi đó (P) đi qua M (0;-1;0) và có cặp véctơ chỉ phương ![]()
Gọi ![]() là VTPT của (P). Khi đó
là VTPT của (P). Khi đó ![]()
Phương trình (P): -8x+3y+2z+3=0
Gọi H là giao điểm của đường thẳng d₂ và (P):
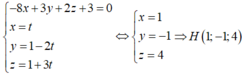
Đường thẳng d đi qua H và có VTCP ![]() có phương trình:
có phương trình:


Đường thẳng d1 qua điểm ![]() đường thẳng d2 qua điểm
đường thẳng d2 qua điểm ![]() Ta có
Ta có ![]() chéo nhau hoặc cắt nhau. Để d1, d2 cắt nhau điều kiện là
chéo nhau hoặc cắt nhau. Để d1, d2 cắt nhau điều kiện là
![]()
![]()
![]() (luôn đúng).
(luôn đúng).
Vậy với mọi m hai đường thẳng đã cho luôn cắt nhau.
Chọn đáp án D.

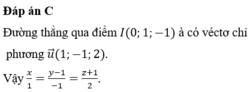


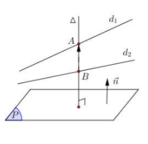

Xét vị trí của d và d1, d và d2.
Đáp án C