Trong không gian với hệ tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng ∆ 1 : x - 1 1 = y 2 = z - 3 - 1 và ∆ 2 : x - 2 2 = y - 3 4 = z - 5 - 2
A. Trùng nhau
B. Song song
C. Chéo nhau
D. Cắt nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
d 1 : x - 1 2 = y 1 = z + 2 - 2 có 1 véc tơ chỉ phương là: u 1 → 2 , 1 , - 2
d 2 : x + 2 - 2 = y - 1 - 1 = z 2 có 1 véc tơ chỉ phương là: u 2 → - 2 , - 1 , 2
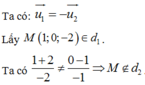
Vậy d 1 d 2 là hai đường thẳng song song
Chọn C

Đáp án B
Ta có
u 1 → = 2 ; 3 ; 2 , u 2 → − 2 ; 2 ; − 3 , M 1 1 ; − 2 ; 2 , M 2 − 2 ; 2 ; 3 .
u 1 → , u 2 → . M 1 M 2 → = 57 ≠ 0.
Vậy d 1 và d 2 chéo nhau.

Đáp án A
Đường thẳng d có véc-tơ chỉ phương ![]() = (3;-1;-2) và đi qua điểm M(-1;0;1).
= (3;-1;-2) và đi qua điểm M(-1;0;1).
Đường thẳng d' có véc-tơ chỉ phương ![]() =(-3;1;2).
=(-3;1;2).
Hai véc-tơ ![]() và
và ![]() cùng phương và điểm M không thuộc đường thẳng d'.
cùng phương và điểm M không thuộc đường thẳng d'.
Do đó hai đường thẳng d và d' song song với nhau.

Đáp án B
Đường thẳng d 1 đi qua điểm M 1 (2; 0; -1) và có vectơ chỉ phương là u 1 → = (4; -6; -8);
đường thẳng d 2 đi qua điểm M 2 (7; 2; 0) và có vectơ chỉ phương là u 2 → = (-6; 9; 12).
Do hai vectơ u 1 → và u 2 → cùng phương nên các đáp án A và C là sai.
Thay tọa độ điểm M 1 vào d 2 , ta thấy:
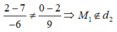
Do đó hai đường thẳng d 1 và d 2 song song.
Vậy đáp án B là đúng.

Đáp án A.
Ta có u 1 = 2 ; - 1 ; 1 và u 2 = - 2 ; 1 ; - 1 suy ra u 1 → = - u 2 → .
Mặt khác M ( 3 ; 1 ; 2 ) ∈ d 1 và M ∈ d 2 suy ra d 1 và d 2 trùng nhau.