Tìm tất cả các giá trị thực của tham số m để hàm số y = mx 4 + ( m - 1 ) x 2 + 2 có đúng 1 điểm cực đại và không có điểm cực tiểu.
A. ![]() .
.
B. 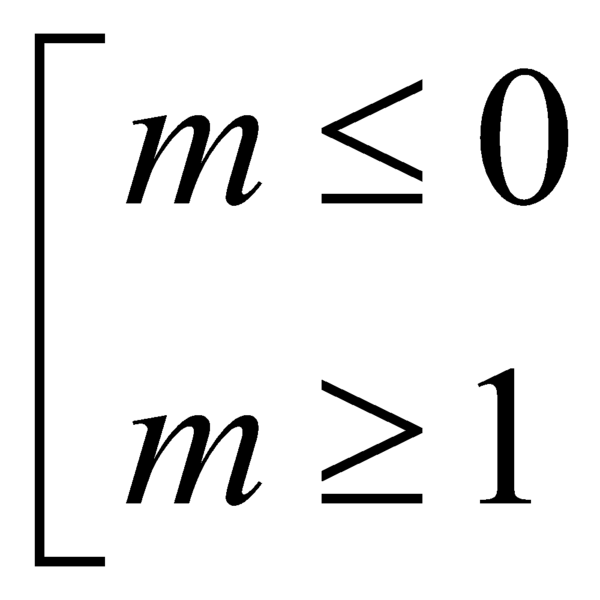 .
.
C. ![]() .
.
D. ![]() .
.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm có 2 cực tiểu và 1 cực đại khi:
\(\left\{{}\begin{matrix}m>0\\2\left(m-1\right)m< 0\end{matrix}\right.\)
\(\Rightarrow0< m< 1\)

Chọn D
Ta có y ' = 3 x 2 - 6 m x + m - 1
Hàm số có cực đại, cực tiểu khi và chỉ khi PT y ' = 0 có hai nghiệm phân biệt
Điều này tương đương
![]()
Hai điểm cực trị có hoành độ dương
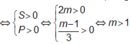
Vậy các giá trị cần tìm của m là m >1

Chọn C
[Phương pháp tự luận]
![]()

Hàm số có cực đại , cực tiểu khi và chỉ khi m < 1
Tọa độ điểm cực trị A ( 0 ; m + 1 )
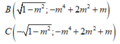
![]()
Phương trình đường thẳng BC: y + m 4 - 2 m 2 - m = 0
![]()
![]()
![]()
Vậy S đạt giá trị lớn nhất ⇔ m = 0
[Phương pháp trắc nghiệm]
![]()
![]()
![]()
![]()
Vậy S đạt giá trị lớn nhất ⇔ m = 0

Ta có
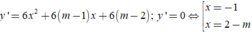
Để hàm số có hai cực trị kh y’=0 có hai nghiệm phân biệt
⇔ 2 - m ≠ - 1 ⇔ m ≠ 3
● Nếu -1<2-m hay m<3,
ycbt 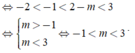
● Nếu 2-m<-1 hay m>3, ycbt
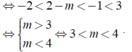
Vậy m ∈ - 1 ; 3 ∪ 3 ; 4
Chọn A.
Đáp án C
TH1: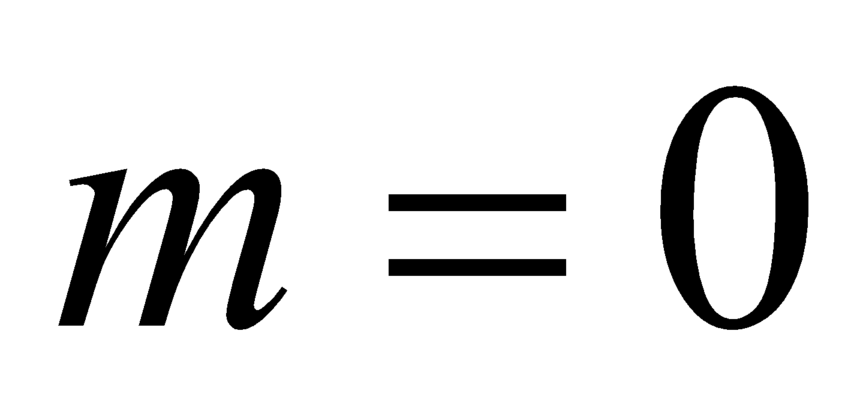 suy ra
suy ra 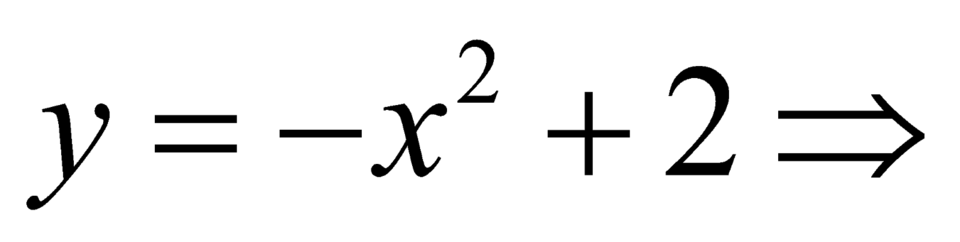 hàm số có
hàm số có 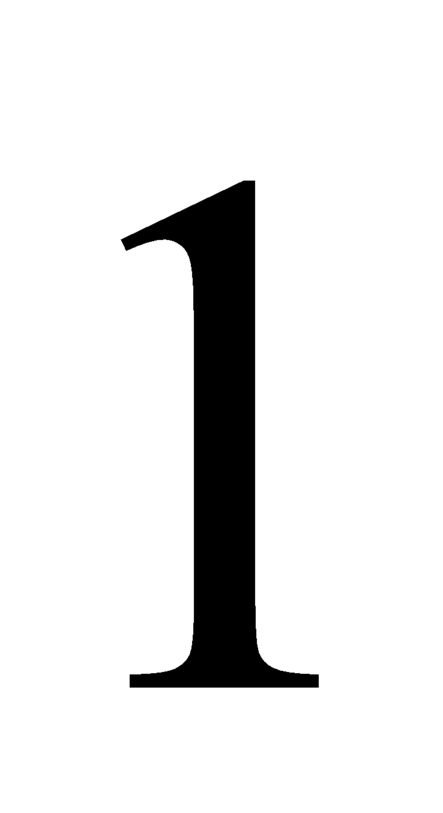 điểm cực đại
điểm cực đại  nhận m=0.
nhận m=0.
TH2: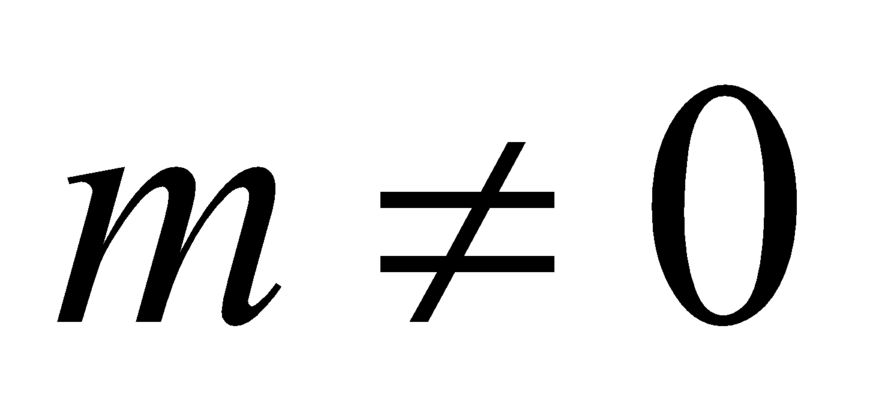 .
.
Theo yêu cầu bài toán
Vậy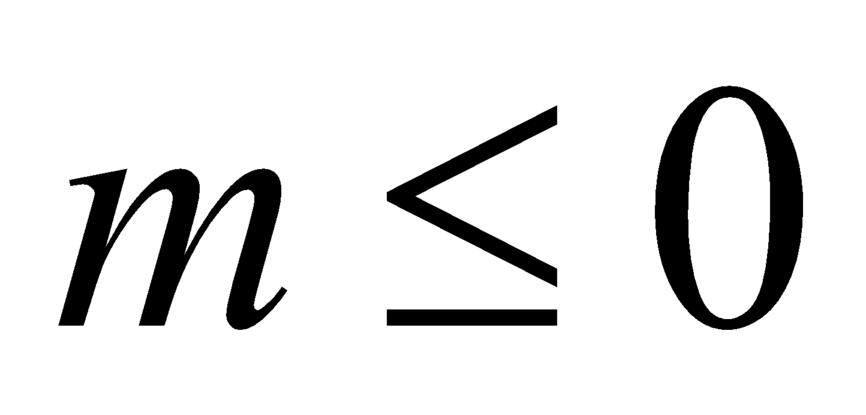 là giá trị cần tìm.
là giá trị cần tìm.