Bất phương trình m x 2 - 2 ( m + 1 ) x + m + 7 < 0 vô nghiệm khi:
A . m ≥ 1 5
B . m > 1 4
C . m > 1 5
D . m > 1 25
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn


a.
Pt có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(-m+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\2m^2+7m+7>0\left(\text{luôn đúng}\right)\end{matrix}\right.\)
\(\Rightarrow m\ne-1\)
b.
BPT vô nghiệm khi \(\left(m^2-4m-5\right)x^2+2\left(m-5\right)-1< 0\) nghiệm đúng với mọi x
- Với \(m=-1\) ko thỏa mãn
- Với \(m=5\) thỏa mãn
- Với \(m\ne\left\{-1;5\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-4m-5< 0\\\Delta'=\left(m-5\right)^2+m^2-4m-5< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\\left(m-5\right)\left(2m-4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\2< m< 5\end{matrix}\right.\) \(\Rightarrow2< m< 5\)
Kết hợp lại ta được: \(2< m\le5\)

\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)

Xét \(f_{\left(x\right)}=m\left(m+8\right)x^2+2\left(m+8\right)x+9m+1\ge0\)
\(\Leftrightarrow\left(m^2+8m\right).x^2+2\left(m+8\right).x+9m+1\ge0\)
Để bpt vô nghiệm \(\left\{{}\begin{matrix}m^2+8m< 0\\9m^3-72m^2+8m+64< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3< m< 0\\\left\{{}\begin{matrix}-3< m< \approx\dfrac{-3}{\sqrt{10}}\\m< \approx\dfrac{-3}{\sqrt{10}}\end{matrix}\right.\end{matrix}\right.\)
=> \(-8< m< -\dfrac{3}{\sqrt{10}}\)

Lười làm lắm cứ xét từng khoản là được
Đầu tiên giải bất thứ nhất
Ở bất thứ 2 xét 2 trường hợp
- TH 1: \(m\le0\)
- TH2: \(m>0\)
+ \(\hept{\begin{cases}m-x^2>0\\x+m< 0\end{cases}}\)
+\(\hept{\begin{cases}m-x^2< 0\\x+m>0\end{cases}}\)
Chọn A.
ĐK: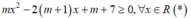
TH1: m = 0:
TH2:
Vậy BPT đã cho vô nghiệm khi m ≥ 1 5