Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp đáy một góc
60
∘
. Gọi M là điểm đối xứng với C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện. Tính thể tích V A.
V
=
7
6
a
3
36
B.
V
=
7
6
a
3
72
C.
V
=
5
6
a
3
...
Đọc tiếp
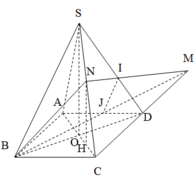
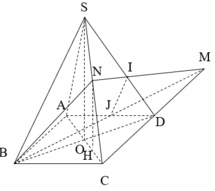
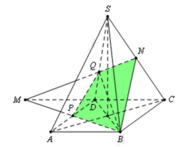
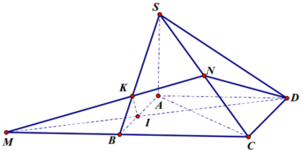
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp đáy một góc 60 ∘ . Gọi M là điểm đối xứng với C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện. Tính thể tích V
A. V = 7 6 a 3 36
B. V = 7 6 a 3 72
C. V = 5 6 a 3 72
D. V = 5 6 a 3 36
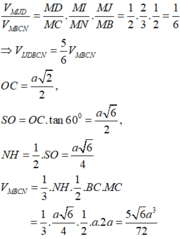
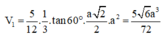
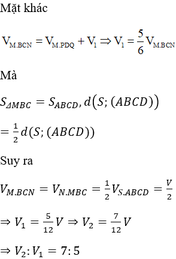
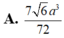
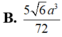
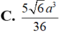
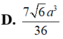
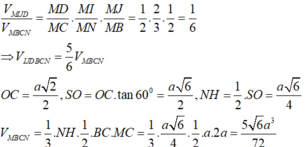
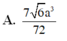
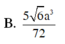
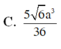
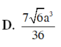
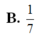
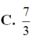
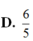
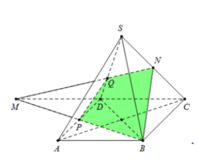
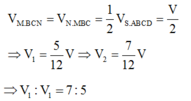
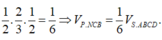
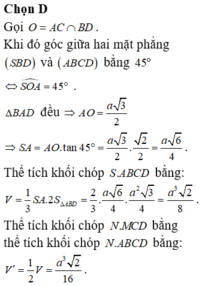
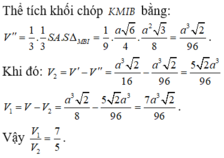
Đáp án C
Ta có: 2 O D 2 = a 2 ⇒ O D = a 2
⇒ S O = O D tan 60 ∘ = a 2 . 3 = a 3 2
Gọi H là hình chiếu của N lên (ABCD) là trung điểm của OC.
Ta có: N H = S O 2 = a 6 4 ; S M B C = S A B C D = a 2
V N . B C M = 1 3 N H . S M B C = 1 3 . a 6 4 . a 2 = a 3 6 12
Ta có:
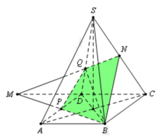
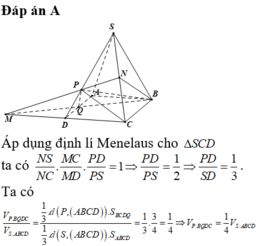
M D D C . C S C N . N P P M = 1 ⇔ 1.2. N P P M = 1 ⇔ N P P M = 1 2 ⇒ P M M N = 2 3
Ta có: V M . D P Q V M . B C N = P M M N . M D M C . M Q M B = 2 3 . 1 2 . 1 2 = 1 6
⇒ V N p Q D C A = 5 6 V N . B C M = 5 6 . a 3 6 12 = 5 a 3 6 72