Cho 2 đường thẳng d 1 : x - 1 1 = y + 1 2 = z - 2 ; d 2 : x + 2 - 1 = y - 1 = z - 3 1 . Viết phương trình mặt phẳng (P) chứa (d1) và (P) // (d2).
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay lần lượt tọa độ các điểm vào phương trình đường thẳng ta thấy tọa độ của Q không thỏa mãn phương trình. Vậy điểm Q không thuộc đường thẳng d.
Chọn D

Đáp án D
Phương pháp:
Thay tọa độ các điểm vào phương trình đường thẳng và kiểm tra tọa độ đó có thỏa mãn phương trình hay không.
Cách giải
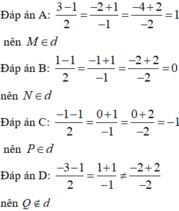

Chọn A.
Gọi ∆ là đường thẳng cần tìm
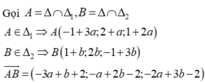
Đường thẳng d có vecto chỉ phương a d → = 0 ; 1 ; 1
![]()
![]()
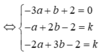
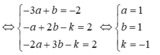
Ta có A(2;3;3); B(2;2;2)
∆ đi qua điểm A(2;3;3) và có vectơ chỉ phương ![]()
Vậy phương trình của ∆ là

Chọn A
Mặt phẳng (P) có vectơ pháp tuyến là n → =(1;1;1)
Gọi ∆ là đường thẳng cần tìm và
![]()
![]()
![]()
![]()
Ta có
![]()
![]()
![]()
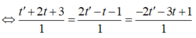
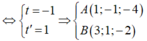

Đáp án C
Gọi B 2 + t ; - 1 - t ; 1 + t A B ¯ = 1 + t ; - t ; t - 2 . Cho A B ¯ . u d ¯ = 0 ⇔ t + 1 - 4 t - 2 t + 4 = 0 ⇔ t = 1 ⇒ A B ¯ = 2 ; - 1 ; - 1
Khi đó d : x - 1 2 = y + 1 - 1 = z - 3 - 1 .
Chọn đáp án D