Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y = x 3 + ( m + 2 ) x 2 + ( m 2 m - 3 ) x - m 2 cắt trục hoành tại ba điểm phân biệt?
A. 3
B.. 4
C. 1
D. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 2 2018
Chọn đáp án A
Phương pháp
Nhẩm nghiệm của phương trình hoành độ giao điểm, từ đó tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.
Để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt thì phương trình x 2 + ( m + 3 ) x + m 2 = 0 phải có hai nghiệm phân biệt khác 1
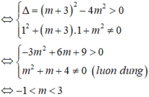
Do đó với -1<m<3 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
CM
8 tháng 7 2018
Chọn đáp án C.
Ta có y ' = 3 x 2 - 2 ( m + 1 ) x + m 2 - 2
trước tiên ta phải có phương trình y ' = 0 có hai nghiệm phân biệt
Điều kiện hai điểm cực trị của đồ thị hàm số nằm cùng về một phía đối với trục hoành là y x 1 . y x 2 > 0
⇔ y = 0 có đúng một nghiệm thực.
Thử trực tiếp các giá trị của m∈{−1,0,1,2} nhận các giá trị m∈{−1,0,2} để y = 0 có đúng một nghiệm thực.
AH
Akai Haruma
Giáo viên
14 tháng 2 2017
Lời giải:
Đồ thị hàm số \(y=-x^4+2(m+2)x^2-(4+m)\) không có điểm chung với trục hoành nghĩa là phương trình \(x^4-2(m+2)x^2+(m+4)= 0\) vô nghiệm
Đặt \(x^2=t\). Khi đó ta cần tìm $m$ nguyên sao cho \(t^2-2(m+2)t+(m+4)=0(1)\) vô nghiệm
Sẽ có hai kiểu xảy ra:
Kiểu 1: \((1)\) có \(\Delta'=(m+2)^2-(m+4)=m^2+3m<0\Leftrightarrow -3< m<0\)
Vì \(m\in\mathbb{Z}\Rightarrow m\in \left \{ -1,-2 \right \}\)
Kiểu 2: \((1)\) có nghiệm nhưng hai nghiệm đó là hai nghiệm âm( Kết hợp với \(t\geq 0\) sẽ suy ra mâu thuẫn, phương trình vô nghiệm)
Trước tiên \(\Delta'=m^2+3m\geq 0\Rightarrow \) \(\left[\begin{matrix}m\ge0\\m\le-3\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{\begin{matrix} t_1+t_2=2(m+2)<0 \\ t_1t_2=m+4> 0\end{matrix}\right.\Rightarrow -4< m<-2\Rightarrow m=-3\)
Vậy \(m\in \left \{-1,-2,-3\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)
CM
15 tháng 10 2018
Hàm số g(x) nghịch biến trên khoảng (0;1) khi 
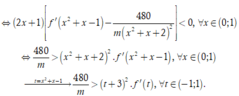
Dựa vào đồ thị, ta có
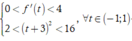
Theo YCBT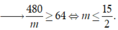 
Chọn C.
Đáp án là A
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành:
Đồ thị hàm số đã cho cắt trục hoành tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ⇔ (2) có 2 nghiệm phân biệt khác 1
Do đó có 3 giá trị nguyên của m thỏa mãn ycbt.