Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a, gọi α là góc giữa đường thẳng AB' và mặt phẳng (BB'D'D). Tính sin α .
A. 3 4 .
B. 3 2 .
C. 3 5 .
D. 1 2 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ B B ' D ' D
=> B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
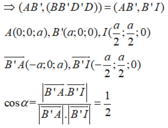

Đáp án C
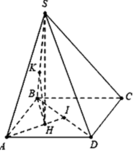
Gọi H là tâm đường tròn ngoại tiếp đều ∆ABD
Ta có 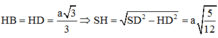
Lại có d(H;(SBC)) = HK và 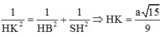
Khoảng cách từ D →(SBC) là 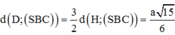
Vậy ∆ABD ![]()
Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ ( B B ' D ' D ) ⇒ B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)