Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
Ta có
Vì f'(x) luôn đồng biến trên
ℝ
nên 
, do đó: a > 0 và b > 0
Mặt khác vì đồ thị hàm số không cắt trục Ox nên chọn đáp án D.
+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
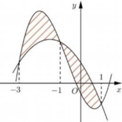
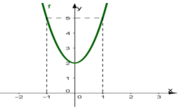
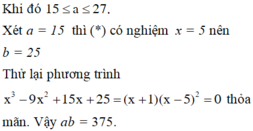
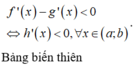
Phương trình hoành độ giao điểm của (C) và (P) là
x 3 + a x 2 + b x + c = m x 2 + n x + p
⇔ x 3 + a - m x 2 + b - n x + c - p = 0 *
Dựa vào đồ thị ta thấy hai đồ thị hàm số tiếp xúc nhau tại điểm có hoành độ x=-1 và cắt nhau tại điểm có hoành độ x=1 nên phương trình (*) có nghiệm x=-1 (bội 2) và x=1 (nghiệm đơn).
Viết lại (*) ta được x + 1 2 x - 1 = 0
Vậy
Chọn đáp án B.