Viết phương trình mặt phẳng song song với (P): 6x -2y + 3z + 7 = 0 và tiếp xúc với mặt cầu x 2 + y 2 + z 2 +2x+2y+2z - 1 = 0
A. 6x - 2y + 3z - 8 = 0
B. 6x - 2y + 3z - 3 = 0
C. 6x - 2y + 3z -7 = 0
D. 6x - 2y + 3z - 5 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 6 2019
Đáp án C
Gọi (Q) là mặt phẳng cần tìm. Vì (Q) song song với (P) nên phương trình (Q) có dạng
Tâm mặt cầu I(-1;-1;-1) bán kính R = 2
Vì (Q) tiếp xúc với mặt cầu nên d(I,(Q)) = R hay
CM
1 tháng 4 2018
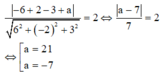
Chọn C.
Trên mặt phẳng (Q): x + 2y - 2z + 1 = 0 chọn điểm M (-1;0;0).
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng: x + 2y - 2z + D = 0 với D ≠ 1.
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z + 10 = 0 và x + 2y -2z – 8 = 0.
CM
4 tháng 1 2018
Chọn D.
Mặt cầu (S) có tâm I(-1;2;1) và bán kính
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng:
x + 2y – 2z + D = 0 với D ≠ 1.
Vì (P) tiếp xúc với mặt cầu (S) nên d(I;(P)) = R = 3
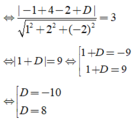
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z – 10 = 0 và x + 2y – 2z + 8 = 0
CM
31 tháng 3 2019
Chọn C.
Phương pháp: Lần lượt tìm các yếu tố tâm và bán kính của mặt cầu.
Cách giải: Tọa độ tâm mặt cầu thỏa mãn hệ
7 tháng 4 2016
Mặt phẳng (P) có vec tơ pháp tuyến \(\overrightarrow{n}=\left(1;1;-2\right);\overrightarrow{AB}=\left(-2;1;-1\right)\)
Ta có \(\left[\overrightarrow{n};\overrightarrow{AB}\right]=\left(1;5;3\right)\)
(Q) vuông góc với (P), song song với đường thẳng AB suy ra (Q) có vectơ pháp tuyến là \(\left[\overrightarrow{n_1};\overrightarrow{AB}\right]=\left(1;5;3\right)\) nên phương trình mặt phẳng (Q) có dạng \(x+5y+3z+m=0\)
Mặt cầu (S) có tâm \(I\left(1;-1;1\right)\), bán kính R = 3
Mặt phẳng (Q) tiếp xúc với (S) có \(d\left(I,\left(Q\right)\right)=R\Leftrightarrow\frac{\left|1-5+3+m\right|}{\sqrt{35}}\)
\(\Leftrightarrow\left|m-1\right|=3\sqrt{35}\Leftrightarrow\begin{cases}m=1+3\sqrt{35}\\m=1-3\sqrt{35}\end{cases}\)
- Với \(m=1+3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1+3\sqrt{35}=0\)
- Với \(m=1-3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1-3\sqrt{35}=0\)
Chọn C
Gọi (Q) là mặt phẳng cần tìm. Vì (Q) song song với (P) nên phương trình (Q) có dạng
6x - 2y + 3z + a = 0
Tâm mặt cầu I(-1;-1;-1) bán kính R = 2
Vì (Q) tiếp xúc với mặt cầu nên d(I,(Q))=R hay