Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: AB → = (−4; 5; −1) và AC → = (0; −1; 1) suy ra n → = AB → ∧ n → = (4; 4; 4)
Do đó (ABC) có vecto pháp tuyến là n → = (4; 4; 4) hoặc n ' → = (1; 1; 1)
Suy ra phương trình của (ABC) là: (x – 5) + (y – 1) + (z – 3) = 0 hay x + y + z – 9 =0
Vecto pháp tuyến của mặt phẳng (ACD) vuông góc với hai vecto A C → = 0 ; - 1 ; 1 v à A D → = - 1 ; - 1 ; 3
Chọn D.
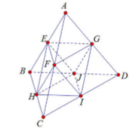
Giả sử khối tứ diện là ABCD. Gọi E, F, G, H, I, J lần lượt là trung điểm của AB. AC, AD, BC, CD, BD.
Ta có 
Do đó 
Vậy 
Đáp án A
Gọi M,N,P,Q,H,R lần lượt là trung điểm của SA,SC,BC,AB,AC,SB
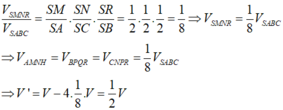
Đáp án A
Gọi M,N,P,Q,H,R lần lượt là trung điểm của SA,SC,BC,AB,AC,SB
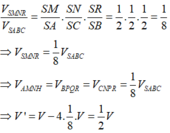
Chọn D.
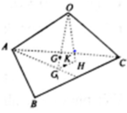
Gọi G1 là trọng tâm của tam giác ABC, H và K lần lượt là hình chiếu của O và G trên mặt phẳng (ABC). Khi đó
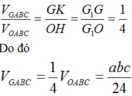
Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là a/2. Khi đó
Từ đó suy ra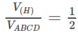 
Chọn B