Cho hàm số y = 0,2 x 2 và y = x.
Vẽ hai đồ thị của những hàm số này trên cùng một mặt phẳng tọa độ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
- Vẽ đường thẳng y = -x + 6
Cho x = 0 ⇒ y = 6 được điểm (0, 6)
Cho y = 0 ⇒ x = 6 được điểm (6, 0)
⇒ Đường thẳng y = -x + 6 đi qua các điểm (6; 0) và (0; 6).
- Lập bảng giá trị và vẽ đồ thị hàm số 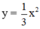
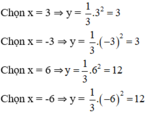
⇒ Parabol đi qua các điểm (3; 3); (-3; 3); (-6; 12); (6; 12); (0; 0).
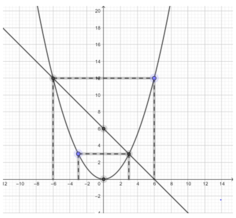
b)Xét phương trình hoành độ giao điểm


b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}0,2x^2-x=0\\y=x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(0,2x-1\right)=0\\y=x\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;1\right);\left(5;5\right)\right\}\)

- Vẽ đường thẳng y = -x + 6
Cho x = 0 ⇒ y = 6 được điểm (0, 6)
Cho y = 0 ⇒ x = 6 được điểm (6, 0)
⇒ Đường thẳng y = -x + 6 đi qua các điểm (6; 0) và (0; 6).
- Lập bảng giá trị và vẽ đồ thị hàm số 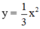
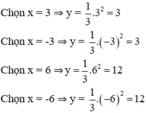
⇒ Parabol đi qua các điểm (3; 3); (-3; 3); (-6; 12); (6; 12); (0; 0).
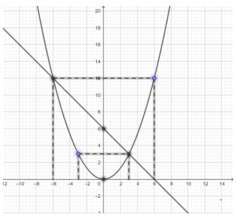

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2=-2x+3\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+2x-3=0\\y=x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+3\right)\left(x-1\right)=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(-3;9\right);\left(1;1\right)\right\}\)

a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì
Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot4^2=4\)
\(\Leftrightarrow a\cdot16=4\)
hay \(a=\dfrac{1}{4}\)
a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)
\(\Rightarrow a=\dfrac{1}{4}\)
b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)
- Ta có đồ thì của hai hàm số :
c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)

\(a,y=\dfrac{1}{4}x^2\)
Cho \(x=1=>y=\dfrac{1}{4}\\ x=2=>y=1\\ x=3=>y=\dfrac{9}{4}\\ x=4=>y=4\\ x=5=>y=\dfrac{25}{4}\)
Vẽ đồ thị đi qua các điểm \(\left(1;\dfrac{1}{4}\right);\left(2;1\right);\left(3;\dfrac{9}{4}\right);\left(4;4\right);\left(2;\dfrac{25}{4}\right)\)
\(y=x-1\)
\(Cho\) \(x=0=>y=-1\) ta được điểm \(\left(0;-1\right)\)
Cho \(y=0=>x=1\) ta được điểm \(\left(1;0\right)\)
Vẽ đồ thị đi qua hai điểm \(\left(0;-1\right);\left(1;0\right)\)
b, Hoành độ giao điểm của hai hàm số là nghiệm của pt
\(\dfrac{1}{4}x^2=x-1\\ < =>\dfrac{1}{4}x^2-x+1=0\\ < =>x=2\)
Thay \(x=2\) vào \(y=x-1\)
\(\Leftrightarrow y=2-1=1\)
Vậy tọa độ giao điểm là \(\left(2;1\right)\)
Lời giải:
a. Bạn có thể tự vẽ
b. PT hoành độ giao điểm: $\frac{1}{4}x^2=x-1$
$\Leftrightarrow x^2=4(x-1)$
$\Leftrightarrow x^2-4x+4=0$
$\Leftrightarrow (x-2)^2=0\Leftrightarrow x=2$
Với $x=2$ thì $y=x-1=2-1=1$
Vậy tọa độ giao điểm của 2 đths là $(2,1)$

\(a,-1< 0\Leftrightarrow\left(d'\right)\text{ nghịch biến trên }R\\ b,\text{PT hoành độ giao điểm: }x=-x+2\Leftrightarrow x=1\Leftrightarrow y=1\Leftrightarrow A\left(1;1\right)\\ \text{Vậy }A\left(1;1\right)\text{ là giao 2 đths}\\ c,\text{3 đt đồng quy }\Leftrightarrow A\left(1;1\right)\in\left(d''\right)\\ \Leftrightarrow m-1+2m=1\\ \Leftrightarrow3m=2\Leftrightarrow m=\dfrac{2}{3}\)

a: 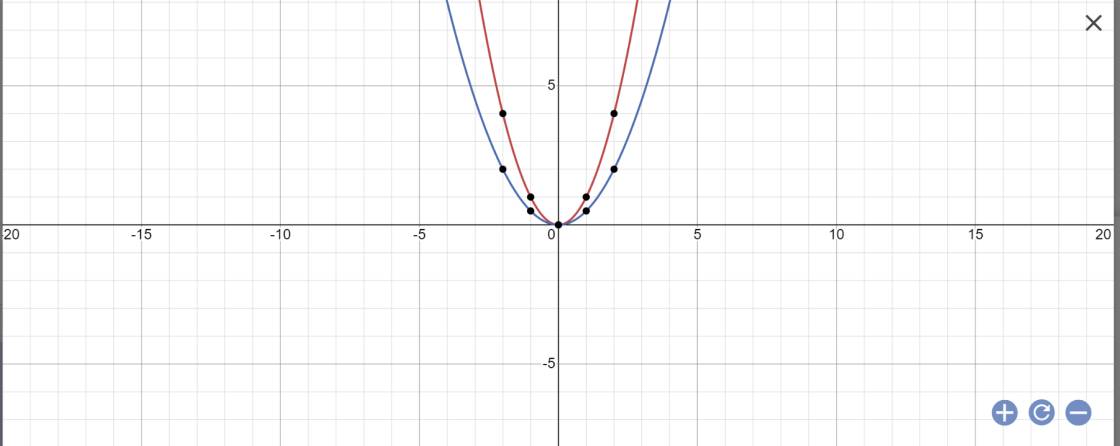
b: Khi x=2 thì y=1/2*2^2=2
=>A(2;2)
Khi x=2 thì y=2^2=4
=>B(2;4)
c: Tọa độ A' là:
\(\left\{{}\begin{matrix}x_{A'}=-x_A=-2\\y_{A'}=y_A=2\end{matrix}\right.\)
Vì f(-2)=1/2*(-2)^2=2
nên A' thuộc (P1)
Tọa độ B' là:
\(\left\{{}\begin{matrix}x_{B'}=-x_B=-2\\y_{B'}=y_B=4\end{matrix}\right.\)
Vì f1(-2)=(-2)^2=4
nên B' thuộc y=x^2
Đồ thị hàm số y = 0,2 x 2
*Các giá trị của x và y :
*Đồ thị hàm số y = x đi qua gốc tọa độ O và điểm (1;1).