ai giúp mình làm bài với 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1:
1: \(\left(2a+b\right)^2=4a^2+4ab+b^2\)
2: \(\left(a-3b\right)^2=a^2-6ab+9b^2\)
4: \(\left(3x-5y\right)^2=9x^2-30xy+25y^2\)
7: \(\left(3x-1\right)^2=9x^2-6x+1\)
9: \(\left(x+\dfrac{1}{2}\right)^2=x^2+x+\dfrac{1}{4}\)
10: \(\left(3x-\dfrac{1}{2}\right)^2=9x^2-3x+\dfrac{1}{4}\)
11: \(\left(4-\dfrac{1}{2}x\right)^2=16-4x+\dfrac{1}{4}x^2\)
12: \(\left(3x-0.5\right)^2=9x^2-3x+\dfrac{1}{4}\)
13: \(\left(4x-0.25\right)^2=16x^2-2x+\dfrac{1}{16}\)



Câu 4:
1. Hiển nhiên $AD\parallel BC$. Áp dụng định lý Talet:
$\frac{BM}{AN}=\frac{PM}{PN}$
$\frac{CM}{NE}=\frac{PM}{PN}$
$\Rightarrow \frac{BM}{AN}=\frac{CM}{NE}$. Mà $BM=CM$ do $M$ là trung điểm $BC$ nên $AN=NE$. $N$ thì nằm giữa $A,E$ (dễ cm)
Do đó $N$ là trung điểm $AE$
2.
Xét tam giác $ABC$ và $DCA$ có:
$\widehat{ABC}=\widehat{DCA}=90^0$
$\widehat{BCA}=\widehat{CAD}$ (so le trong)
$\Rightarrow \triangle ABC\sim \triangle DCA$ (g.g)
3. Theo định lý Pitago:
Từ tam giác đồng dạng phần 2 suy ra:
$\frac{AC}{DA}=\frac{BC}{CA}$
$\Rightarrow AD=\frac{AC^2}{BC}=\frac{6^2}{4}=9$ (cm)
4,Theo phần 1 thì:
$\frac{PM}{PN}=\frac{BM}{AN}=\frac{CM}{AN}$
Mà cũng theo định lý Talet: $\frac{CM}{AN}=\frac{QM}{QN}$
$\Rightarrow \frac{PM}{PN}=\frac{QM}{QN}$
(đpcm)

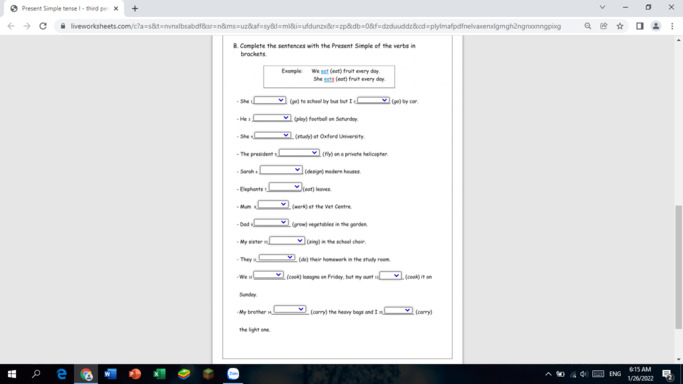
1. goes - go
2. plays
3. studies
4. flies
5. designs
6. eat
7. works
8. grows
9. sings
10. do
11. cook - cooks
12. carries - carry

a, 4,78+x=5,6 <=> x=5,6-4,78 = 0,82
b, x-3,92=0,61 <=> x = 3,92 + 0,61 = 4,53
c, 7-x=4,52 <=> x = 7-4,52 = 2,48
a: =>x=5,6-4,78=0,82
b: =>x=0,61+3,92=4,53
c: =>x=7-4,52=2,48
d: =>x=17,1:4,5=3,8
e: =>x=17,1x4,5=76,95
f: =>x=42,16:6,2=6,8


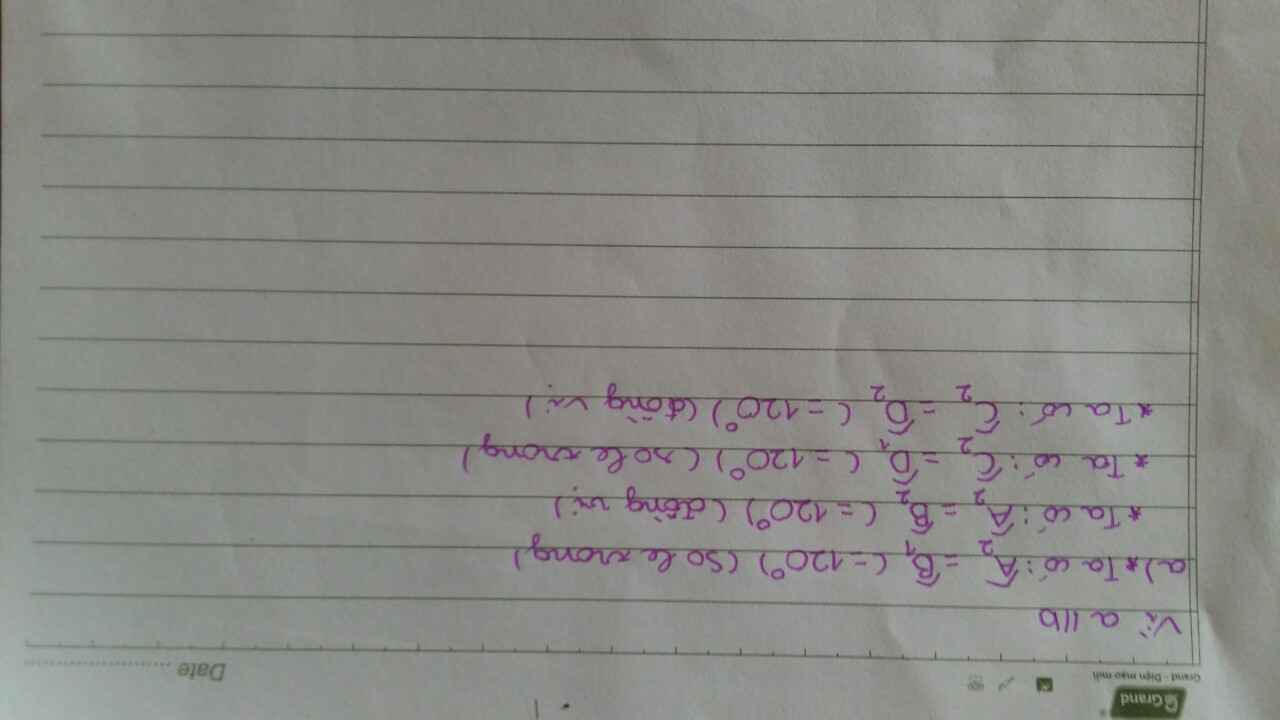
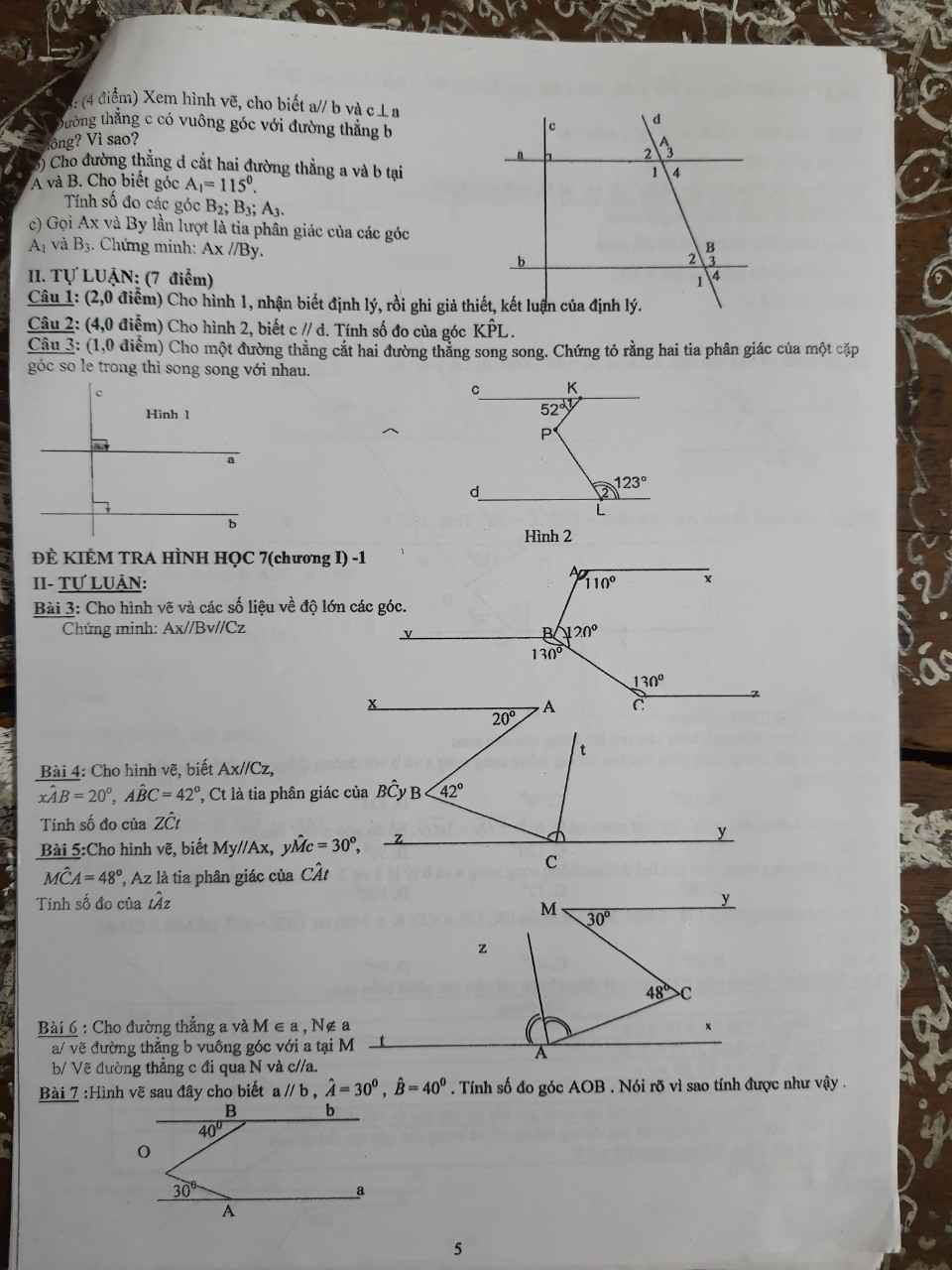



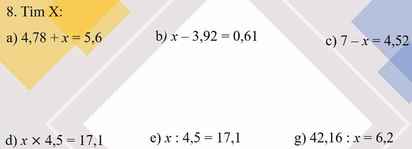
 ai làm giúp mình bài này với
ai làm giúp mình bài này với
nhanh lê mình đang gấp
các bạn có thể cho mình cách giải được không]