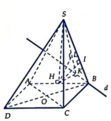
Cho hình chóp S.ABCD có S A ⊥ A B C D , A B C D là hình chữ nhật. S A = A D = 2 a . Góc giữa (SBC)và mặt đáy ABCD là 60 ° . Gọi G là trọng tâm tam giác SBC. Thể tích khối chóp S.AGD là
A. 32 a 3 3 27
B. 8 a 3 3 27
C. 4 a 3 3 9
D. 16 a 3 9 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?

Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.

a: (SB;(ABCD))=(BS;BA)=góc SBA
AC=căn a^2+3a^2=2a
SA=căn SC^2-AC^2=a*căn 3
tan SBA=SA/AB=căn 3
=>góc SBA=60 độ
b: (SC;(SAD))=(SC;SD)=góc SCD
SD=căn SA^2+AD^2=2a*căn 3
cos SCD=(CS^2+CD^2-SD^2)/(2*CS*CD)=-2/căn 7
=>góc SCD=139 độ

Đáp án B.
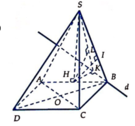
Vẽ đường thẳng d qua B và song song với AC.
Gọi K, I lần lượt là hình chiếu của H trên d và SB, L là hình chiếu của H trên SK.
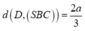
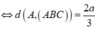
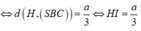
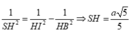
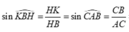
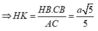
![]()
![]()
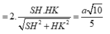

Đáp án B.
Vẽ đường thẳng d qua B và song song với AC.
Gọi K, I lần lượt là hình chiếu của H trên d và SB, L là hình chiếu của H trên SK.
d ( D , ( S B C ) ) = 2 a 3 ⇔ d A ; ( A B C ) = 2 a 3 ⇔ d H , S B C = a 3 ⇔ H I = a 3
1 S H 2 = 1 H I 2 - 1 H B 2 ⇒ S H = a 5 5
sin K B H ⏞ = H K H B = sin C A B ⏞ = C B A C ⇒ H K = H B . C B A C = a 5 5
d A C ; S B = d A , S B K = 2 d H , S B K = 2 H L = 2 . S H . H K S H 2 + H K 2 = a 10 5

a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)
Đáp án B
Gọi M là trung điểm của BC ta có: S G S M = 2 3
Do B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ S B A ⇒ S B A ^ = S B C ; A B C ^ = 60 ∘
Ta có: A B tan 60 ∘ = S A ⇒ A B = 2 a 3 .
S A M B = 1 2 A B . A D = 2 a 2 3 ⇒ V S . A M D = 1 3 S A . S A M B = 4 a 3 3 9 V S . A M D = 2 3 V S . A M D = 8 3 a 3 27