Cho đường thẳng y = (m – 2)x + n (m ≠ 2). (d)
Tìm các giá trị của m và n trong mỗi trường hợp sau:
Đường thẳng (d) cắt đường thẳng y = 1/2x - 3/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 1 2019
Ta có: y = -1,5x + 0,5. ( d 2 )
Đường thẳng (d): y = (m – 2)x + n song song với ( d 2 ) khi:
m – 2 = -1,5 và n ≠ 0,5
hay m = 0,5 và n ≠ 0,5.
Trả lời: (d) song song với ( d 2 ) khi m = 0,5 và n ≠ 0,5.
CM
20 tháng 5 2018
Ta có: y = 2x – 3 ( d 3 )
Đường thẳng (d) trùng với ( d 3 ) khi m – 2 = 2 và n = -3
Hay m = 4 và n = -3.
Trả lời: Khi m = 4 và n = -3 thì hai đường thẳng (d) và ( d 3 ) trùng nhau.
7 tháng 12 2021
Vì (d)//y=x-3 nên m-2=1
hay m=3
Thay x=0 và y=5 vào y=x+n, ta được:
n+0=5
hay n=5
CM
7 tháng 5 2019
Đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 - 2 2 nên ta có n = 1 - 2
Đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 2 + 2 nên ta có:
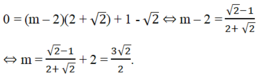
Trả lời: Khi n = 1 -
2
và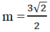 
thì đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 -
2
và cắt trục hoành tại điểm có hoành độ 2 +
2
CM
16 tháng 9 2019
Đường thẳng y = (m – 2)x + n (d) đi qua hai điểm A(-1;2) và B(3; -4). Khi đó tọa độ các điểm A, B thỏa mãn (d), nghĩa là:
2 = (m – 2)(-1) + n (1)
và -4 = (m – 2).3 + n (2)
Rút gọn hai phương trình (1) và (2), ta được
-m + n = 0; (1’)
3m + n = 2. (2’)
Từ (1’) suy ra n = m. Thay vào (2’), ta có 3m + 3 = 2 suy ra m = 1/2.
Trả lời: Khi m = n = 1/2 thì (d) đi qua hai điểm A và B đã cho.
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 3 2023
a.
Phương trình hoành độ giao điểm:
\(x^2+6x+3=-2mx-m^2\Leftrightarrow x^2+2\left(m+3\right)x+m^2+3=0\)
\(\Delta'=\left(m+3\right)^2-\left(m^2+3\right)=6\left(m+1\right)>0\Rightarrow m>-1\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-2\left(m+3\right)\\x_Ax_B=m^2+3\end{matrix}\right.\)
\(P=10\left(m+3\right)-2\left(m^2+3\right)=-2m^2+10m+24\)
\(P=-2\left(m-\dfrac{5}{2}\right)^2+\dfrac{73}{2}\le\dfrac{73}{2}\)
\(P_{max}=\dfrac{73}{2}\) khi \(m=\dfrac{5}{2}\)
b.
Pt hoành độ giao điểm:
\(x^2-2x-2=x+m\Leftrightarrow x^2-3x-m-2=0\)
\(\Delta=9+4\left(m+2\right)>0\Rightarrow m>-\dfrac{17}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=3\\x_Ax_B=-m-2\end{matrix}\right.\)
Đồng thời \(y_A=x_A+m\) ; \(y_B=x_B+m\)
\(P=OA^2+OB^2=x_A^2+y_A^2+x_B^2+y_B^2\)
\(=x_A^2+x_B^2+\left(x_A+m\right)^2+\left(x_B+m\right)^2\)
\(=2\left(x_A^2+x_B^2\right)+2m\left(x_A+x_B\right)+2m^2\)
\(=2\left(x_A+x_B\right)^2-4x_Ax_B+2m\left(x_A+x_B\right)+2m^2\)
\(=18-4\left(-m-2\right)+6m+2m^2\)
\(=2m^2+10m+26=2\left(m+\dfrac{5}{2}\right)^2+\dfrac{27}{2}\ge\dfrac{27}{2}\)
Dấu "=" xảy ra khi \(m=-\dfrac{5}{2}\)
14 tháng 5 2023
Để hai đường cắt nhau trên trục tung thì n+5=1 và m-3<>-2
=>n=-4 và m<>1
LD
14 tháng 5 2023
Để hai đường cắt nhau trên trục tung thì n+5=1 và m-3<>-2
=>n=-4 và m<>1
19 tháng 3 2022
(d) // (d') : y = -x + 3
\(\left\{{}\begin{matrix}m+3=-1\\n-2\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-4\\n\ne5\end{matrix}\right.\)
<=> (d) : \(y=-x+n-2\)
Thay x = -2 vào (d'') : y = 3x + 4
<=> y = -6 + 4 = -2
Vậy (d) cắt (d'') tại A(-2;-2)
<=> -2 = 2 + n - 2 <=> n = -2 (tmđk)
Vậy (d) : y = -x -4
Ta có: y = 0,5x – 1,5. (d1)
Đường thẳng (d) và ( d 1 ) khi m – 2 ≠ 0,5, còn n lấy giá trị tùy ý. Suy ra (d) cắt ( d 1 ) khi m ≠ 2,5 còn n tùy ý.
Trả lời: (d) cắt ( d 2 ) khi m ≠ 2,5 còn n tùy ý.