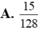
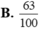
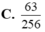
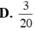
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
Mỗi bước người này có 2 lựa chọn sang trái hoặc phải nên số phần tử không gian mẫu là 2 10 .
Để sau đúng 10 bước người này quay lại đúng gốc tọa độ O thì người này phải sang trái 5 lần và sang phải 5 lần, do đó số cách bước trong 10 bước này là C 10 5 .
Xác suất cần tính bằng 
.
Đáp án D
Phương pháp :
Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng => | Ω |
Gọi A là biến cố : « Quân vua sau 3 bước trở về đúng vị trí ban đầu » . Tính |A| .
Cách giải :
Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng => | Ω | = 8 3 .
Gọi A là biến cố : « Quân vua sau 3 bước trở về đúng vị trí ban đầu »
TH1: Quân vua di chuyển bước thứ nhất sang ô đen liền kề (được tô màu đỏ) có 4
cách.
Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 4 cách.
Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.
Vậy TH này có 4.4 = 16 cách.
TH2: Quân vua di chuyển bước thứ nhất sang các ô trắng liền kề (được tô màu đỏ) có
4 cách.
Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 2 cách.
Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.
Vậy TH này có 4.2 = 8 cách
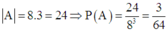
Chọn A
Không gian mẫu là 8 3
Có hai trường hợp
+ Trường hợp 1: Bước 1 đi 4 ô góc thì bước 2 có 2 cách đi, bước 3 có 1 cách đi
+ Trường hợp 2: Bước 1 đi 4 ô còn lại thì bước 2 có 4 cách đi, bước 3 có 1 cách đi
Vậy tât cả có 4.2 + 4.4 = 24
Suy ra xác suất để sau 3 bước đi quân vua trở về ô ban đầu là: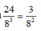 
a) Vị trí máy bay vào lúc 14 giờ 30 phút là: \(\left\{ \begin{array}{l}x = \frac{{1600}}{3} - \frac{{1400}}{3}.\frac{1}{2} = 300\\y = \frac{{1900}}{3} - \frac{{1400}}{3}.\frac{1}{2} = 400\end{array} \right.\)
Vậy tọa độ máy bay là \(\left( {300;400} \right)\). Thời điểm này máy bay đã xuất hiện trên màn hình ra đa.
b) Ta có: \(MO = \sqrt {{{\left( {\frac{{1600}}{3} - \frac{{1400}}{3}t} \right)}^2} + {{\left( {\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)}^2}} \).
Do có \(M{O_{\min }} = 50\sqrt 2 \Leftrightarrow t = \frac{5}{4}\).
Vậy sau khi bay \(\frac{5}{4} = 1,25\) (giờ) tức là lúc 15h15p thì máy bay gần ra đa nhất và khoảng cách từ ra đa đến máy bay khi đó là \(50\sqrt 2 \left( {km} \right)\).
c) Máy bay rời khỏi màn hình ra đa khi mà khoảng cách từ M đến O lớn hơn 500km tức là:
\(MO = \sqrt {{{\left( {\frac{{1600}}{3} - \frac{{1400}}{3}t} \right)}^2} + {{\left( {\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)}^2}} \ge 500 \Leftrightarrow \left[ \begin{array}{l}t = \frac{1}{2}\\t = 2\end{array} \right.\)
Vậy sau khi bay được 2h tức là lúc 16h thì máy bay thoát khỏi màn hình ra đa.
