Cho với x, y là số phức thỏa mãn điều kiện . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức . Tính M+m.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

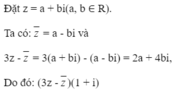
= 2a - 4b + (2a + 4b)i - 5(a + bi) = 8i - 1
Theo giả thiết: (2a - 4b) + (2a + 4b)i - 5(a + bi) = 8i - 1
⇔ -3a - 4b + (2a - b)i = -1 + 8i
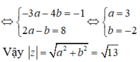
Chọn C

Đáp án D
Cách giải: gọi z=x+yi
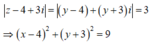
Vậy quỹ tích các điểm z thuộc đường tròn tâm I(4;-3); R=3
Đặt 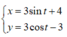
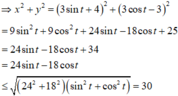
(theo bunhiacopxki)
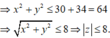

Đặt z = a + bi(a, b ∈ R). Ta có
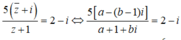
⇔ 5a - 5(b - 1)i = (2 - i)(a + 1 + bi)
⇔ 3a - b - 2 + (a - 7b + 6)i = 0
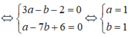
Suy ra z = 1 + i và w = 1 + ( 1 + i ) + ( 1 + i ) 2 = 2 + 3 i .
Vậy: | w | = ( 4 + 9 ) = 13
Chọn B

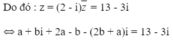
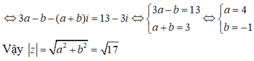


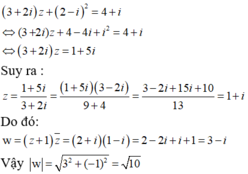
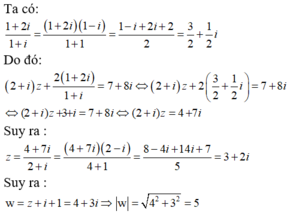
Đáp án B.