Tập nghiệm của phương trình l o g 2 ( x 2 - 1 ) = l o g 2 ( 2 x ) là
A. S = 1 + 2 2
B. S = 1 + 2
C. S = 1 + 2 ; 1 - 2
D. S = 2 ; 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

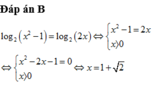

\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)
\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)
\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)
\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)
\(\Leftrightarrow VT\le2g\left(x\right)\)
Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)
\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)
Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)
Ta có:
\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)
\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)
Vậy tập nghiệm của pt đã cho có đúng 1 phần tử

(2): B
(3):
a) Phương trình -5x-1=0 có tập nghiệm là \(S=\left\{\frac{-1}{5}\right\}\)
b) Phương trình \(9x^2+16=0\) có tập nghiệm là \(\varnothing\)
c) Phương trình 2(x-1)=2(x+1) có tập nghiệm là: \(x\in\varnothing\)
d) Phương trình \(\left(x+2\right)^2=x^2+4x+4\) có tập nghiệm là \(x\in R\)
(4): Không có câu nào đúng

a/ pt x = 2 có tập hợpnghiệm là S = {2}b/ pt vô nghiệm có tậphợp nghiệm là S = ∅

Ta có:
\({x^2} - 2x - 3 = 0 \Leftrightarrow (x + 1)(x - 3) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right. \Rightarrow E = \{ - 1;3\} \)
Lại có: \((x + 1)(2x - 3) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \frac{3}{2}\end{array} \right.\)
\( \Rightarrow G = \left\{ { - 1;\frac{3}{2}} \right\}\)
\( \Rightarrow P = E \cap G = \left\{ { - 1} \right\}\).
Xét phương trình \(x^2-2x-3=0\) có: \(a-b+c=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{c}{a}=3\end{matrix}\right.\Rightarrow E=\left\{-1;3\right\}.\)
Xét phương trình \(\left(x+1\right)\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+1=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\Rightarrow G=\left\{-1;\dfrac{3}{2}\right\}.\)
\(\Rightarrow P=E\cap G=\left\{-1\right\}.\)

Câu 6 :
a ) Hai phương trình không tương đương . Bởi lẽ :
\(x^2-4=0\Leftrightarrow\left(x-2\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\) ( Nhận 2 nghiệm ) . Còn phương trình kia chỉ nhận 1 nghiệm
b ) Hai phương trình không tương đương . Bởi vì :
\(x-3=0\Rightarrow x=3\) ( một nghiệm)
\(x^2+1=0\Leftrightarrow x^2=-1\) vô lí ( vô nghiệm )

(x - 1)2 + (x - 2)2 = 1 (1)
\(\Leftrightarrow\) x2 - 2x + 1 + x2 - 4x + 4 - 1 = 0
\(\Leftrightarrow\) 2x2 - 6x + 4 = 0
\(\Leftrightarrow\) 2(x2 - 3x + 2) = 0
\(\Leftrightarrow\) x2 - 3x + 2 = 0
\(\Leftrightarrow\) x2 - 2x - x + 2 = 0
\(\Leftrightarrow\) x(x - 2) - (x - 2) = 0
\(\Leftrightarrow\) (x - 2)(x - 1) = 0
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\)
Vậy S = {2; 1}
x4 - 3x3 + 3x2 - 3x + 2 = 0 (2)
\(\Leftrightarrow\) x4 - 3x3 + 3x2 - x - 2x + 2 = 0
\(\Leftrightarrow\) x(x3 - 3x2 + 3x - 1) - 2(x - 2) = 0
\(\Leftrightarrow\) x(x - 1)3 - 2(x - 1) = 0
\(\Leftrightarrow\) (x - 1)[x(x - 1) - 2] = 0
\(\Leftrightarrow\) (x - 1)(x2 - x - 2) = 0
\(\Leftrightarrow\) (x - 1)(x2 - 2x + x - 2) = 0
\(\Leftrightarrow\) (x - 1)[x(x - 2) + (x - 2)] = 0
\(\Leftrightarrow\) (x - 1)(x - 2)(x + 1) = 0
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-1\end{matrix}\right.\)
Vậy S = {1; 2; -1}
x3 - 7x + 6 = 0 (3)
\(\Leftrightarrow\) x3 - x - 6x + 6 = 0
\(\Leftrightarrow\) x(x2 - 1) - 6(x - 1) = 0
\(\Leftrightarrow\) x(x - 1)(x + 1) - 6(x - 1) = 0
\(\Leftrightarrow\) (x - 1)[x(x + 1) - 6] = 0
\(\Leftrightarrow\) (x - 1)(x2 + x - 6) = 0
\(\Leftrightarrow\) (x - 1)(x2 + x + \(\frac{1}{4}\) - \(\frac{25}{4}\)) = 0
\(\Leftrightarrow\) (x - 1)[(x + \(\frac{1}{2}\))2 - \(\frac{25}{4}\)] = 0
\(\Leftrightarrow\) (x - 1)(x + \(\frac{1}{2}\) - \(\frac{5}{2}\))(x + \(\frac{1}{2}\) + \(\frac{5}{2}\)) = 0
\(\Leftrightarrow\) (x - 1)(x - 2)(x + 3) = 0
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-3\end{matrix}\right.\)
Vậy S = {1; 2; -3}
Mình phân tích thế thôi, chứ câu hỏi bạn đặt ra mình không hiểu!
Chúc bn học tốt!!