Biết I = ∫ 1 5 2 x - 1 2 x + 3 2 x - 1 + 1 d x = a + b ln 2 + c ln 3 5 a , b , c ∈ ℤ . Khi đó, giá trị P = a 2 - a b + 2 c là:
A. 10
B. 8
C. 9
D. 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Bất phương trình đã cho tương đương với hệ sau:
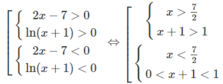
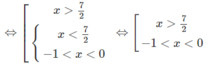
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
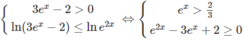
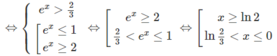
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )

`a)TXĐ:R\\{1;1/3}`
`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`
`b)TXĐ:R`
`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`
`c)TXĐ: (4;+oo)`
`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`
`d)TXĐ:(0;+oo)`
`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`
`e)TXĐ:(-oo;-1)uu(1;+oo)`
`y'=-7x^[-8]-[2x]/[x^2-1]`
Lời giải:
a.
$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$
$=-4(3x^2-4x+1)^{-5}(6x-4)$
$=-8(3x-2)(3x^2-4x+1)^{-5}$
b.
$y'=(3^{x^2-1})'+(e^{-x+1})'$
$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$
$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$
c.
$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$
$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$
d.
\(y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2\)
\(=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}\)
e.
\(y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}\)

a) \(\int\dfrac{2dx}{x^2-5x}=\int\left(\dfrac{-2}{5x}+\dfrac{2}{5\left(x-5\right)}\right)dx=-\dfrac{2}{5}ln\left|x\right|+\dfrac{2}{5}ln\left|x-5\right|+C\)
\(\Rightarrow A=-\dfrac{2}{5};B=\dfrac{2}{5}\Rightarrow2A-3B=-2\)
b) \(\int\dfrac{x^3-1}{x+1}dx=\int\dfrac{x^3+1-2}{x+1}dx=\int\left(x^2-x+1-\dfrac{2}{x+1}\right)dx=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2+x-2ln\left|x+1\right|+C\)
\(\Rightarrow A=\dfrac{1}{3};B=\dfrac{1}{2};E=-2\Rightarrow A-B+E=-\dfrac{13}{6}\)

\(a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}\)
\(c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}\)

\(A=x^2-4x+1\)
\(A=\left(x^2-4x+4\right)-3\)
\(A=\left(x-2\right)^2-3\)
Vì \(\left(x-2\right)^2\ge0\) với mọi x
\(\Rightarrow\left(x-2\right)^2-3\ge-3\) với mọi x
\(\Rightarrow Amin=-3\Leftrightarrow x=2\)
\(B=4x^2+4x+11\)
\(B=\left(4x^2+4x+1\right)+10\)
\(B=\left(2x+1\right)^2+10\)
Vì \(\left(2x+1\right)^2\ge0\) với mọi x
\(\Rightarrow\left(2x+1\right)^2+10\ge10\) với mọi x
\(\Rightarrow Bmin=10\Leftrightarrow x=-\dfrac{1}{2}\)
\(C=\left(x-1\right)\left(x+3\right)\left(x+2\right)\left(x+6\right)\)
\(C=\left[\left(x-1\right)\left(x+6\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]\)
\(C=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(C=\left(x^2+5x\right)^2-36\)
Vì \(\left(x^2+5x\right)^2\ge0\) với mọi x
\(\Rightarrow\left(x^2+5x\right)^2-36\ge-36\)
\(\Rightarrow Cmin=-36\Leftrightarrow x^2+5x=0\)
\(\Rightarrow x\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(D=5-8x-x^2\)
\(D=-\left(x^2+8x-5\right)\)
\(D=-\left(x^2+8x+16-16-5\right)\)
\(D=-\left(x^2+8x+16\right)+21\)
\(D=-\left(x+4\right)^2+21\)
Vì \(-\left(x+4\right)^2\le0\) với mọi x
\(\Rightarrow-\left(x+4\right)^2+21\le21\) với mọi x
\(\Rightarrow Dmax=21\Leftrightarrow x=-4\)
\(E=4x-x^2+1\)
\(E=-\left(x^2-4x-1\right)\)
\(E=-\left(x^2-4x+4-4-1\right)\)
\(E=-\left(x^2-4x+4\right)+5\)
\(E=-\left(x-2\right)^2+5\)
Vì \(-\left(x-2\right)^2\le0\) với mọi x
\(\Rightarrow-\left(x-2\right)^2+5\le5\) với mọi x
\(\Rightarrow Emax=5\Leftrightarrow x=2\)

a) Điều kiện: \(\left\{{}\begin{matrix}4x+2>0\\x-1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>1\)
Khi đó biến đổi pương trình như sau:
\(\ln\dfrac{4x+2}{x-1}=\ln x\)
\(\Leftrightarrow\dfrac{4x+2}{x-1}=x\)
\(\Leftrightarrow4x+2=x\left(x-1\right)\)
\(\Leftrightarrow x^2-5x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{5+\sqrt{33}}{2}\\x_2=\dfrac{5-\sqrt{33}}{2}\left(loại\right)\end{matrix}\right.\)
Vậy nghiệm của phương trình là: \(x=\dfrac{5+\sqrt{33}}{2}\)
b) Điều kiện: \(\left\{{}\begin{matrix}3x+1>0\\x>0\end{matrix}\right.\)
Hay là: \(x>0\)
Biến đổi phương trình như sau:
\(\log_2\left(3x+1\right)\log_3x-2\log_2\left(3x+1\right)=0\)
\(\Leftrightarrow\log_2\left(3x+1\right)\left(\log_3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\log_2\left(3x+1\right)=0\\\log_3x=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+1=2^0\\x=3^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=9\end{matrix}\right.\)
Vậy nghiệm là x = 9.

a) \(\left(x-3\right)\left(x+3\right)=\left(x-2\right)^2-1\)
\(\Leftrightarrow x^2-9=x^2-4x+4-1\)
\(\Leftrightarrow4x=12\)
\(\Leftrightarrow x=3\)
b) \(\left(2x-1\right)^2=\left(2x+5\right)\left(2x-5\right)+2\)
\(\Leftrightarrow4x^2-4x+1=4x^2-25+2\)
\(\Leftrightarrow4x=24\)
\(\Leftrightarrow x=6\)
c) \(\left(x+1\right)^3=x^2\left(x-2\right)+5\left(x^2-1\right)\)
\(\Leftrightarrow x^3+3x^2+3x+1=x^3-2x^2+5x^2-5\)
\(\Leftrightarrow3x=-6\)
\(\Leftrightarrow x=-2\)
d) \(\left(x^2-3x+9\right)\left(x+3\right)=\left(x-2\right)^3+\left(3x-1\right)\left(2x+3\right)\)
\(\Leftrightarrow x^3+3^3=x^3-6x^2+12x-8+6x^2+7x-3\)
\(\Leftrightarrow x^3+27=x^3+19x-11\)
\(\Leftrightarrow19x=38\)
\(\Leftrightarrow x=2\)

a) \(\left(x+8\right)\left(x+6\right)=104+x^2\Leftrightarrow x^2+6x+8x+48=104+x^2\)
\(\Leftrightarrow x^2+6x+8x-x^2=104-48\Leftrightarrow14x=56\Leftrightarrow x=\dfrac{56}{14}=4\)
vậy \(x=4\)
b) \(\left(x+1\right)\left(x+2\right)-\left(x-3\right)\left(x+4\right)=6\)
\(\Leftrightarrow x^2+2x+x+2-\left(x^2+4x-3x-12\right)=6\)
\(\Leftrightarrow x^2+2x+x+2-x^2-4x+3x+12=6\)
\(\Leftrightarrow2x+14=6\Leftrightarrow2x=6-14=-8\Leftrightarrow x=\dfrac{-8}{2}=-4\)
vậy \(x=-4\)
c) \(4x\left(x-5\right)-\left(x-1\right)\left(4x-3\right)=5\)
\(\Leftrightarrow4x^2-20x-\left(4x^2-3x-4x+3\right)=5\)
\(\Leftrightarrow4x^2-20x-4x^2+3x+4x-3=5\)
\(\Leftrightarrow-13x-3=5\Leftrightarrow-13x=5+3=8\Leftrightarrow x=\dfrac{8}{-13}=\dfrac{-8}{13}\)
vậy \(x=\dfrac{-8}{13}\)
d) \(\left(3x-4\right)\left(x-2\right)=3x\left(x-9\right)-3\)
\(\Leftrightarrow3x^2-6x-4x+8=3x^2-27x-3\)
\(\Leftrightarrow3x^2-6x-4x-3x^2+27x=-3-8\)
\(\Leftrightarrow17x=-11\Leftrightarrow x=\dfrac{-11}{17}\) vậy \(x=\dfrac{-11}{17}\)
e) câu này đề bị thiếu rồi nha bn
f) \(5x\left(x-3\right)=\left(x-2\right)\left(5x-1\right)-5\)
\(\Leftrightarrow5x^2-15x=5x^2-x-10x+2-5\)
\(\Leftrightarrow5x^2-15x-5x^2+x+10x=2-5\)
\(\Leftrightarrow-4x=-3\Leftrightarrow x=\dfrac{-3}{-4}=\dfrac{3}{4}\) vậy \(x=\dfrac{3}{4}\)
a) \(\left(x+8\right)\left(x+6\right)=104+x^2\)
\(\Leftrightarrow x^2+14x+48=104+x^2\)
\(\Leftrightarrow14x=56\)
\(\Rightarrow x=4\)
b) \(\left(x+1\right)\left(x+2\right)-\left(x-3\right)\left(x+4\right)=6\)
\(\Leftrightarrow x^2+3x+2-x^2-7x+12=6\)
\(\Leftrightarrow-4x=-8\)
\(\Rightarrow x=2\)
c) \(4x\left(x-5\right)-\left(x-1\right)\left(4x-3\right)=5\)
\(\Leftrightarrow4x^2-20x-4x^2+3x+4x-3=5\)
\(\Leftrightarrow-13x=8\)
\(\Rightarrow x=\dfrac{-8}{13}\)
d) \(\left(3x-4\right)\left(x-2\right)=3x\left(x-9\right)-3\)
\(\Leftrightarrow3x^2-10x+8=3x^2-27x-3\)
\(\Leftrightarrow17x=-11\)
\(\Rightarrow x=\dfrac{-11}{17}\)
e) \(\left(x-5\right)\left(x-4\right)-\left(x+1\right)\left(x-2\right)=7\)
\(\Leftrightarrow x^2-9x+20-x^2+x+2=7\)
\(\Leftrightarrow-8x=-15\)
\(\Rightarrow x=\dfrac{15}{8}\)
f) \(5x\left(x-3\right)=\left(x-2\right)\left(5x-1\right)-5\)
\(\Leftrightarrow5x^2-15x=5x^2-11x+2-5\)
\(\Leftrightarrow-4x=-3\)
\(\Rightarrow x=\dfrac{3}{4}\)

Giải như sau.
(1)+(2)⇔x2−2x+1+√x2−2x+5=y2+√y2+4⇔(x2−2x+5)+√x2−2x+5=y2+4+√y2+4⇔√y2+4=√x2−2x+5⇒x=3y(1)+(2)⇔x2−2x+1+x2−2x+5=y2+y2+4⇔(x2−2x+5)+x2−2x+5=y2+4+y2+4⇔y2+4=x2−2x+5⇒x=3y
⇔√y2+4=√x2−2x+5⇔y2+4=x2−2x+5, chỗ này do hàm số f(x)=t2+tf(x)=t2+t đồng biến ∀t≥0∀t≥0
Công việc còn lại là của bạn !
\(\left(x+6\right)\left(2x+1\right)=0\)
<=> \(\orbr{\begin{cases}x+6=0\\2x+1=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-6\\x=-\frac{1}{2}\end{cases}}\)
Vậy....
hk tốt
^^
Chọn A.
Phương pháp: Tính tích phân từ đó tìm a, b, c.
Cách giải: Ta tính