Một hộp đựng 10 viên bi trong đó có 4 viên bi đỏ, 3 viên bi xanh, 2 viên bi vàng, 1 viên bi trắng. Lấy ngẫu nhiên 2 bi tính xác suất biến cố 2 viên lấy ra màu đỏ là
A. C 4 2 C 10 2
B. C 5 2 C 10 2
C. C 4 2 C 8 2
D. C 7 2 C 10 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có, số phần tử của không gian mẫu n ( Ω ) = C 10 2
Gọi các biến cố: D: “lấy được 2 viên đỏ” ; X: “lấy được 2 viên xanh” ;
V: “lấy được 2 viên vàng”
Ta có D, X, V là các biến cố đôi một xung khắc và C = D ∪ X ∪ V
P ( C ) = P ( D ) + P ( X ) + P ( V ) = C 4 2 C 10 2 + C 3 2 C 10 2 + C 2 2 C 10 2 = 2 9
Chọn đáp án B

Ta có: số phần tử của không gian mẫu là Ω = C 40 2
Gọi các biến cố: D: “lấy được 2 bi viên đỏ” ta có: n D = C 20 2 = 190 ;
X: “lấy được 2 bi viên xanh” ta có: n X = C 10 2 = 45 ;
V: “lấy được 2 bi viên vàng” ta có: n V = C 6 2 = 15 ;
T: “ lấy được 2 bi màu trắng” ta có: n T = C 4 2 = 6 .
Ta có D,X,V,T là các biến cố đôi một xung khắc và A = D ∪ X ∪ V ∪ T
Suy ra xác xuất để lấy được 2 viên bi cùng màu là:
P A = P D + P X + P V + P T = 256 C 40 2 = 64 195 .
Chọn đáp án D.

Ta có: ![]()
Gọi các biến cố: D: “lấy được 2 bi viên đỏ” ta có ![]()
X: “lấy được 2 bi viên xanh” ta có: ![]()
V: “lấy được 2 bi viên vàng” ta có: ![]()
T: “ lấy được 2 bi màu trắng” ta có : ![]()
Ta có D; X; V; T là các biến cố đôi một xung khắc và A= D ∪ X ∪ V ∪ T
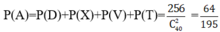
Chọn B.

Số cách chọn 4 viên bi có đúng hai viên bị màu trắng là: ![]()
Suy ra:n(A)=4095.
Chọn C.

Số cách lấy 4 viên bi mà không có viên bi màu đỏ được chọn là:![]()
Suy ra : ![]()
Chọn C.

a) Cách lấy 2 viên bi trong túi là:
Xanh – đỏ; Xanh – trắng; Xanh – vàng; Đỏ - trắng; Đỏ - vàng; Trắng – vàng.
Có 6 cách lấy hai biên bi từ trong túi.
Biến cố \(A\) xảy ra khi 2 viên bi lấy ra có 1 viên bi màu đỏ
Có 3 kết quả thuận lợi cho biến cố \(A\) là Xanh – đỏ; Đỏ - trắng; Đỏ - vàng
Xác suất 2 viên bi lấy ra có 1 viên bi màu đỏ là \(\frac{3}{6} = \frac{1}{2}\).
Vậy xác suất 2 viên bi lấy ra có 1 viên bi màu đỏ là \(\frac{1}{2}\).
b) Biến cố \(B\) xảy ra khi 2 viên bi lấy ra đều không có màu trắng
Có 3 kết quả thuận lợi cho \(B\) là : Xanh – đỏ; Xanh – vàng; Đỏ - vàng.
Xác suất 2 viên bi lấy ra không có viên bi nào màu trắng là \(\frac{3}{6} = \frac{1}{2}\).
Vậy xác suất 2 viên bi lấy ra không có viên bi nào màu trắng là \(\frac{1}{2}\).

Vì 3 viên bi xanh, 4 viên bi đỏ và 5 viên b vàng có kích thước và khối lượng như nhau nên 12 kết quả của phép thử có khả năng xảy ra bằng nhau.
- Biến cố \(A\) xảy ra khi ta lấy được viên bi màu xanh nên có 3 kết quả thuận lợi cho \(A\). Xác suất của biến có \(A\) là:
\(P\left( A \right) = \frac{3}{{12}} = \frac{1}{4}\).
- Biến cố \(B\) xảy ra khi ta lấy được viên bi không có màu vàng nên viên bi lấy được có thể có màu xanh hoặc màu đỏ. Do đó, có 7 kết quả thuận lợi cho \(B\). Xác suất của biến có \(B\) là:
\(P\left( B \right) = \frac{7}{{12}}\).

Không gian mẫu: \(C_{15}^4\)
a.
Số cách lấy 4 viên bi trong đó có 3 viên màu đỏ: \(C_7^3C_8^1\)
Xác suất: \(P=\dfrac{C_7^3.C_8^1}{C_{15}^4}\)
b.
Lấy 4 viên không có viên đỏ nào (lấy từ 8 viên 2 màu còn lại): \(C_8^4\) cách
Lấy 4 viên có ít nhất 1 viên đỏ: \(C_{15}^4-C_8^4\)
Xác suất: \(P=\dfrac{C_{15}^4-C_8^4}{C_{15}^4}\)
c.
Các trường hợp thỏa mãn: (2 đỏ 1 xanh 1 vàng), (1 đỏ 2 xanh 1 vàng), (1 đỏ 1 vàng 2 xanh)
Số cách lấy: \(C_7^2C_5^1C_3^1+C_7^1C_5^2C_3^1+C_7^1C_5^1C_3^2\)
Xác suất: \(P=\dfrac{C_7^2C_5^1C_3^1+C_7^1C_5^2C_3^1+C_7^1C_5^1C_3^2}{C_{15}^4}\)