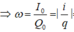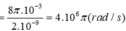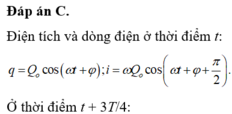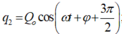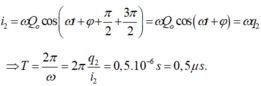Mạch dao động LC đang thực hiện dao động điện từ tự do với chu kì T. Tại thời điểm nào đó cường độ dòng điện trong mạch có độ lớn là 8π (mA), sau đó khoảng thời gian 0,25T thì điện tích trên tụ có độ lớn là 2.10‒9 C. Giá trị của T là
A. 0,5 ms
B. 0,25 ms
C. 0,5 μs
D. 0,25 μs




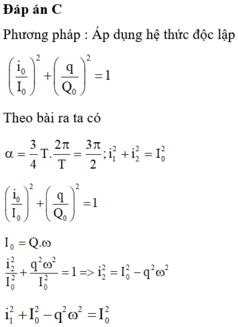
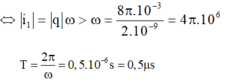


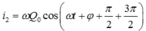
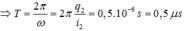
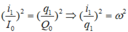
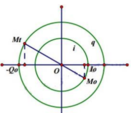
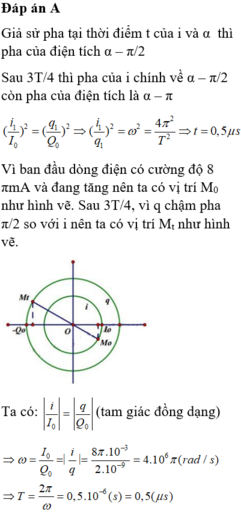
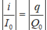 (tam giác đồng dạng)
(tam giác đồng dạng)