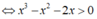Với giá trị nào của x thì biểu thức: f(x) = log 5 ( x 3 - x 2 - 2 x ) xác định?
A . x ∈ ( - 1 ; 0 ) ∪ ( 2 ; + ∞ )
B . x ∈ ( 0 ; 2 ) ∪ ( 4 ; + ∞ )
C . x ∈ ( 0 ; 1 )
D . x ∈ ( 1 ; + ∞ )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn nên viết biểu thức A bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu biểu thức của bạn hơn.

a) Rút gọn E Þ đpcm.
b) Điều kiện xác định E là: x ≠ ± 1
Rút gọn F ta thu được F = 4 Þ đpcm

a. ĐKXĐ: x3 - x \(\ne\)0 <=> x(x2 - 1) \(\ne\)0 <=> x \(\ne\)0 và x\(\ne\)\(\pm\)1
b. \(A=\frac{x\left(x^2+2x+1\right)}{x\left(x-1\right)\left(x+1\right)}\)
\(=\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{x+1}{x-1}với\)\(x\ne0\)và \(x\ne\pm1\)
\(c.A=2\Leftrightarrow\frac{x+1}{x-1}=2\)
\(\Leftrightarrow\left(x-1\right).2=x+1\)
\(2x-2=x+1\)
\(x=3\)
a) Giá trị của phân thức A xác định
\(\Leftrightarrow x^3-x\ne0\)
\(\Leftrightarrow x\left(x^2-1\right)\ne0\)
\(\Leftrightarrow\hept{\begin{cases}x\ne0\\x\ne1\\x\ne-1\end{cases}}\)
Vậy với \(x\ne0;x\ne\pm1\)thì giá trị của phân thức A đưcọ xác định.
ĐKXĐ: \(x\ne0;x\ne\pm1\)
b) Ta có :
\(A=\frac{x^3+2x^2+x}{x^3-x}\)
\(A=\frac{x\left(x^2+2x+1\right)}{x\left(x+1\right)\left(x-1\right)}\)
\(A=\frac{\left(x+1\right)^2}{\left(x+1\right)\left(x-1\right)}\)
\(A=\frac{x+1}{x-1}\)
c) A = 2
\(\Leftrightarrow\frac{x+1}{x-1}=2\)
\(\Leftrightarrow x+1=2\left(x-1\right)\)
\(\Leftrightarrow x+1=2x-2\)
\(\Leftrightarrow x-2x=-1-2\)
\(\Leftrightarrow-x=-3\)
\(\Leftrightarrow x=3\)( Thỏa mãn ĐKXĐ )
Vậy ..............
Chọn A
Biểu thức f(x) = log 5 ( x 3 - x 2 - 2 x ) xác định