Hình vẽ bên là đồ thị của hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e .
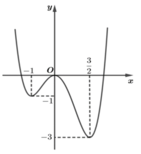
Hỏi có bao nhiêu m nguyên để phương trình f x = m có ít nhất ba nghiệm phân biệt?
A. 1.
B. 2.
C. 3.
D. 4.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
![]()
![]()
![]()
![]()
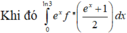
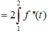

![]()
Do hàm số đạt cực đại tại điểm x=1⇒ f′(1) = 0 và đường thẳng Δ qua hai điểm (0;−3);(1;0) nên có phương trình y=3x−3.
Vì Δ là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 ⇒ f ' ( 2 ) = k △ =3
Vậy
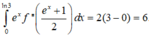

Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’(x) ; ta thấy đồ thị hàm số y= f’(x) là parabol có trục đối xứng là trục tung nên b= 0
+ Đồ thị hàm số y= f’(x) đi qua 2 điểm (1; 5) và (0; 2) ta tìm được: a=1 và c=2.
Suy ra: f’(x) = 3x2+ 2 và f( x) = x3+ 2x+ d,
+ Do đồ thị hàm số (C) đi qua gốc toạ độ nên 0=0+0+ d
Suy ra: d= 0.
Khi đó ta có: f(x) =x3+ 2x và f( 3) –f(2) =21
Chọn D.
Từ đồ thị hàm số (C): y = f(x) ta suy ra đồ thị hàm số (C'): y = f(|x|) như sau:
+) Giữ nguyên phần đồ thị (C) trên miền x ≥ 0 , (kí hiệu phần đồ thị này là C 1 ).
+) Bỏ phần đồ thị (C) ở bên trái trục Oy.
+) Lấy đối xứng C 1 qua trục Oy, (kí hiệu phần đồ thị này là C 2 ).
Khi đó đồ thị của hàm số y = f(|x|) là hợp của hai phần đồ thị C 1 và C 2 .
Ta có đồ thị của hàm số y = f(|x|) như hình vẽ dưới đây:
Chọn C