Cho ∫ 1 e ln x ( l n x x 1 ) 2 d x = a e

PT

Pham Trong Bach

6 tháng 5 2019

Cho ∫ 1 e ln x ( l n x + x + 1 ) 2 d x = a e - 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

6 tháng 5 2019

Đúng(0)

PT

Phạm Trần Phát

18 tháng 11 2023

4. Tính đạo hàm của các hàm số sau:

a) $y = (3x^2-4x+1)^{-4}$

b) $y = 3^{x^2-1} + e^{-x+1}$

c) $y = \ln (x^2-4x) + \log_{3} (2x-1)$

d) $y =x . \ln x + 2^{\frac{x-1}{x+1}}$

e) $y = x^{-7} - \ln (x^2-1)$

#Toán lớp 12

2

2611

18 tháng 11 2023

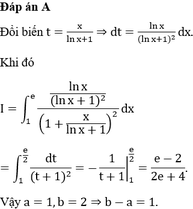
`a)TXĐ:R\\{1;1/3}`

`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`

`b)TXĐ:R`

`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`

`c)TXĐ: (4;+oo)`

`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`

`d)TXĐ:(0;+oo)`

`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`

`e)TXĐ:(-oo;-1)uu(1;+oo)`

`y'=-7x^[-8]-[2x]/[x^2-1]`

Đúng(3)

AH

Akai Haruma

Giáo viên

18 tháng 11 2023

Lời giải:
a.

$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$

$=-4(3x^2-4x+1)^{-5}(6x-4)$

$=-8(3x-2)(3x^2-4x+1)^{-5}$

b.

$y'=(3^{x^2-1})'+(e^{-x+1})'$

$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$

$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$

c.

$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$

$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$

d.

$y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2$

$=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}$

e.

$y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}$

Đúng(3)

B

Buddy

13 tháng 8 2023

Tính đạo hàm cấp hai của mỗi hàm số sau:

a) $y = 2{x^4} - 3{x^3} + 5{x^2}$

b) $y = \frac{2}{{3 - x}}$

c) $y = \sin 2x\cos x$

d) $y = {e^{ - 2x + 3}}$

e) $y = \ln (x + 1)$

f) $y = \ln ({e^x} + 1)$

#Toán lớp 11

3

HQ

Hà Quang Minh

Giáo viên

22 tháng 8 2023

$a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}$

Đúng(1)

HQ

Hà Quang Minh

Giáo viên

22 tháng 8 2023

$c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}$

Đúng(1)

NV

Nguyễn Văn Trí

5 tháng 11 2023

Tính các nguyên hàm.

a)$\int\dfrac{2dx}{x^2-5x}=A\ln\left|x\right|+B\ln\left|x-5\right|+C$ . Tìm 2A-3B.

b)$\int\dfrac{x^3-1}{x+1}$dx=$Ax^3-Bx^2+x+E\ln\left|x+1\right|+C$.Tính A-B+E

#Toán lớp 12

1

NH

Ngọc Hưng

6 tháng 11 2023

a) $\int\dfrac{2dx}{x^2-5x}=\int\left(\dfrac{-2}{5x}+\dfrac{2}{5\left(x-5\right)}\right)dx=-\dfrac{2}{5}ln\left|x\right|+\dfrac{2}{5}ln\left|x-5\right|+C$

$\Rightarrow A=-\dfrac{2}{5};B=\dfrac{2}{5}\Rightarrow2A-3B=-2$

b) $\int\dfrac{x^3-1}{x+1}dx=\int\dfrac{x^3+1-2}{x+1}dx=\int\left(x^2-x+1-\dfrac{2}{x+1}\right)dx=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2+x-2ln\left|x+1\right|+C$

$\Rightarrow A=\dfrac{1}{3};B=\dfrac{1}{2};E=-2\Rightarrow A-B+E=-\dfrac{13}{6}$

Đúng(1)

TC

Tô Cường

20 tháng 2 2020

Câu 1: Cho $\lim\limits_{x\rightarrow e}\frac{\log_2\left(\ln\left(x\right)\right)}{f\left(x\right)}=\frac{1}{\ln\left(2\right)e}$. Biết $\ln\left(f\left(0\right)\right)=1$ và $\int\limits^{5e}_{-e}f\left(2x\right)dx=18e^2$. Tính $\frac{\ln\left(f\left(1+e\right)\right)}{f\left(1+e\right)^{10}}$ bằng: a) 0 b) $\frac{\ln\left(1+e\right)}{\left(1+e\right)^{10}}$ c) $1$ d)...

Đọc tiếp

#Toán lớp 12

0

DD

Đỗ Danh Gia Bảo

10 tháng 10 2021 - olm

Tính các tích phân sau: 1) 2 ln e e x dx  ; 2) 1 3 2 0 4 x dx  x  ; 3) /2 /4 1 tan dx x    ; 4) 1 0 x e dx  ; 5) 2 1 x xe dx    ; 6) 0 1 3 4 dx x    ; 7) 2 1 4 4 5 dx x x      ; 8) 2 0 ln 1 x dx x    (HD: 1 u x  ) ĐS: 1) 2 e ; 2) 16 7 5 3  ; 3) ln 2 ; 4) 2

#Toán lớp 12

0

KD

Kyun Diệp

17 tháng 12 2018

Tìm giá trị NN của biểu thức A,B,C và giá trị LN của biểu thức D,E:

A=x^2-4x+1

B=4x^2+4x+11

C=(x-1)(x+3)(x+2)(x+6)

D=5-8x-x^2

E=4x-x^2+1

#Toán lớp 8

1

TH

Thiên Hàn

17 tháng 12 2018

$A=x^2-4x+1$

$A=\left(x^2-4x+4\right)-3$

$A=\left(x-2\right)^2-3$

Vì $\left(x-2\right)^2\ge0$ với mọi x

$\Rightarrow\left(x-2\right)^2-3\ge-3$ với mọi x

$\Rightarrow Amin=-3\Leftrightarrow x=2$

$B=4x^2+4x+11$

$B=\left(4x^2+4x+1\right)+10$

$B=\left(2x+1\right)^2+10$

Vì $\left(2x+1\right)^2\ge0$ với mọi x

$\Rightarrow\left(2x+1\right)^2+10\ge10$ với mọi x

$\Rightarrow Bmin=10\Leftrightarrow x=-\dfrac{1}{2}$

$C=\left(x-1\right)\left(x+3\right)\left(x+2\right)\left(x+6\right)$

$C=\left[\left(x-1\right)\left(x+6\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]$

$C=\left(x^2+5x-6\right)\left(x^2+5x+6\right)$

$C=\left(x^2+5x\right)^2-36$

Vì $\left(x^2+5x\right)^2\ge0$ với mọi x

$\Rightarrow\left(x^2+5x\right)^2-36\ge-36$

$\Rightarrow Cmin=-36\Leftrightarrow x^2+5x=0$

$\Rightarrow x\left(x+5\right)=0$

$\Rightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.$

$D=5-8x-x^2$

$D=-\left(x^2+8x-5\right)$

$D=-\left(x^2+8x+16-16-5\right)$

$D=-\left(x^2+8x+16\right)+21$

$D=-\left(x+4\right)^2+21$

Vì $-\left(x+4\right)^2\le0$ với mọi x

$\Rightarrow-\left(x+4\right)^2+21\le21$ với mọi x

$\Rightarrow Dmax=21\Leftrightarrow x=-4$

$E=4x-x^2+1$

$E=-\left(x^2-4x-1\right)$

$E=-\left(x^2-4x+4-4-1\right)$

$E=-\left(x^2-4x+4\right)+5$

$E=-\left(x-2\right)^2+5$

Vì $-\left(x-2\right)^2\le0$ với mọi x

$\Rightarrow-\left(x-2\right)^2+5\le5$ với mọi x

$\Rightarrow Emax=5\Leftrightarrow x=2$

Đúng(0)

DH

diệp hoàng

18 tháng 4 2023

( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$

#Toán lớp 12

1

NL

Nguyễn Lê Phước Thịnh

19 tháng 4 2023

Chọn C

Đúng(0)

DH

diệp hoàng

19 tháng 4 2023

em muốn hỏi cách làm ấy ạ? hướng giải là như nào ấy ạ

Đúng(0)

HV

Huỳnh Văn Thiện

20 tháng 2 2018

Cho I = $\int_1^e\dfrac{lnx-1}{x^2-ln^2x}dx$ và t = $\dfrac{lnx}{x}$. Khẳng định nào sau đây là SAI? Vì sao? A. I = $\dfrac{1}{2}\int_0^{\dfrac{1}{e}}\left(\dfrac{1}{t-1}-\dfrac{1}{t+1}\right)dt$ B. I = $\dfrac{1}{2}ln\left(\dfrac{e-1}{e+1}\right)$ C. I = $\int_0^{\dfrac{1}{e}}\dfrac{dt}{1-t^2}$ D. I =...

Đọc tiếp

#Toán lớp 12

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 6 2022

Chọn B

Đúng(0)

NN

Nguyễn Ngọc Thúy Vy

31 tháng 1 2017

giúp em mấy bài nguyên hàm với ạ. huhu 1) cho f(x)=8sin bình(x+pi/12) một nguyên hàm F(x) của f(x) thỏa F(0)=8 là A.4x+2sin(2x+pi/6)+9 B.4x-2sin(2x+pi/6)-9 C.4x+2sin(2x+pi/6)+7 D.4x-2sin(2x+pi/6)+7 2)cho f(x)=x*(e mũ -x) một nguyên hàm F(x) của f(x) thỏa F(0)=1 là A.-(x+1) *(e mũ -x)+1 B.-(x+1)*(e mũ -x)+2 C.(x+1)*(e mũ -x)+1 D.(x+1)*(e mũ -x)+2 e cần bài giải chi tiết ạ. anh chị giúp e với...

Đọc tiếp

#Toán lớp 12

1

AH

Akai Haruma

Giáo viên

31 tháng 1 2017

Lời giải:

Bài 1:

Ta nhớ công thức $\sin^2x=\frac{1-\cos 2x}{2}$. Áp dụng vào bài toán:

$F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx$

$\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})$

$\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c$

Giải thích 1 chút: $d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx$

Vì $F(0)=8\Rightarrow -1+c=8\Rightarrow c=9$

$\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9$

Câu 2:

Áp dụng nguyên hàm từng phần như bài bạn đã đăng:

$\Rightarrow F(x)=-xe^{-x}-e^{-x}+c$

Vì $F(0)=1\Rightarrow -1+c=1\Rightarrow c=2$

$\Rightarrow F(x)=-e^{-x}(x+1)+2$, tức B là đáp án đúng

Đúng(0)

PT

Phạm Trần Phát

19 tháng 1 2024

Tìm các nguyên hàm sau:

a) $\int (3x^2-2x-4)dx $

b) $\int(\sin3x-\cos4x)dx $

c) $\int(e^{-3x}-4^x)dx $

d) $\int\ln(x)dx $

e) $\int(x.e^x)dx $

f) $\int(x+1).\sin(x)dx $

g) $\int x.\ln(x)dx $

#Toán lớp 12

1

NV

Nguyễn Việt Lâm

Giáo viên

19 tháng 1 2024

$\int\left(3x^2-2x-4\right)dx=x^3-x^2-4x+C$

$\int\left(sin3x-cos4x\right)dx=-\dfrac{1}{3}cos3x-\dfrac{1}{4}sin4x+C$

$\int\left(e^{-3x}-4^x\right)dx=-\dfrac{1}{3}e^{-3x}-\dfrac{4^x}{ln4}+C$

d. $I=\int lnxdx$

Đặt $\left\{{}\begin{matrix}u=lnx\\dv=dx\end{matrix}\right.$ $\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x}\\v=x\end{matrix}\right.$

$\Rightarrow u=x.lnx-\int dx=x.lnx-x+C$

e. Đặt $\left\{{}\begin{matrix}u=x\\dv=e^xdx\end{matrix}\right.$ $\Rightarrow\left\{{}\begin{matrix}du=dx\\v=e^x\end{matrix}\right.$

$\Rightarrow I=x.e^x-\int e^xdx=x.e^x-e^x+C$

f.

Đặt $\left\{{}\begin{matrix}u=x+1\\dv=sinxdx\end{matrix}\right.$ $\Rightarrow\left\{{}\begin{matrix}du=dx\\v=-cosx\end{matrix}\right.$

$\Rightarrow I=-\left(x+1\right)cosx+\int cosxdx=-\left(x+1\right)cosx+sinx+C$

g.

Đặt $\left\{{}\begin{matrix}u=lnx\\dv=xdx\end{matrix}\right.$ $\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x}\\v=\dfrac{1}{2}x^2\end{matrix}\right.$

$\Rightarrow I=\dfrac{1}{2}x^2.lnx-\dfrac{1}{2}\int xdx=\dfrac{1}{2}x^2.lnx-\dfrac{1}{4}x^2+C$

Đúng(2)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP