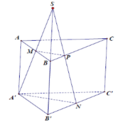
Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có tất cả các cạnh đều bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB và B'C'. Mặt phẳng A ' M N cắt cạnh BC tại P. Tính thể tích V của khối đa diện M B P A ' B ' N
A. V = a 3 3 36
B. V = a 3 3 12
C. V = a 3 7 3 96
D. V = a 3 7 3 48

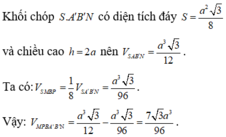
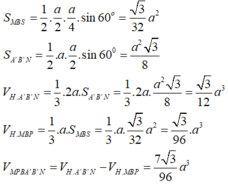
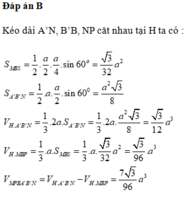
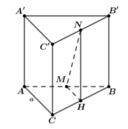
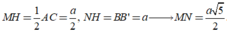
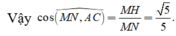
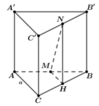
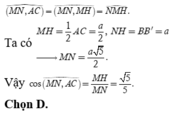
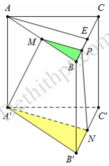
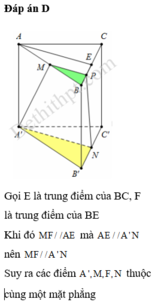

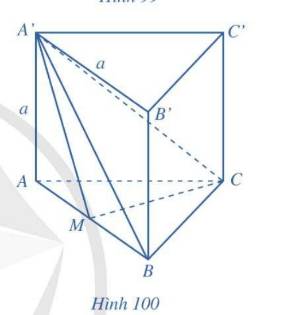
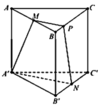
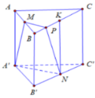
Chọn đáp án C.